Знайти ОДЗ(чому х не може дорівнювати) та знайти х
Вирішити по діях
(6/х²+х)-(х-6/х²-х)+(10/х²-1)=0
Приложения:
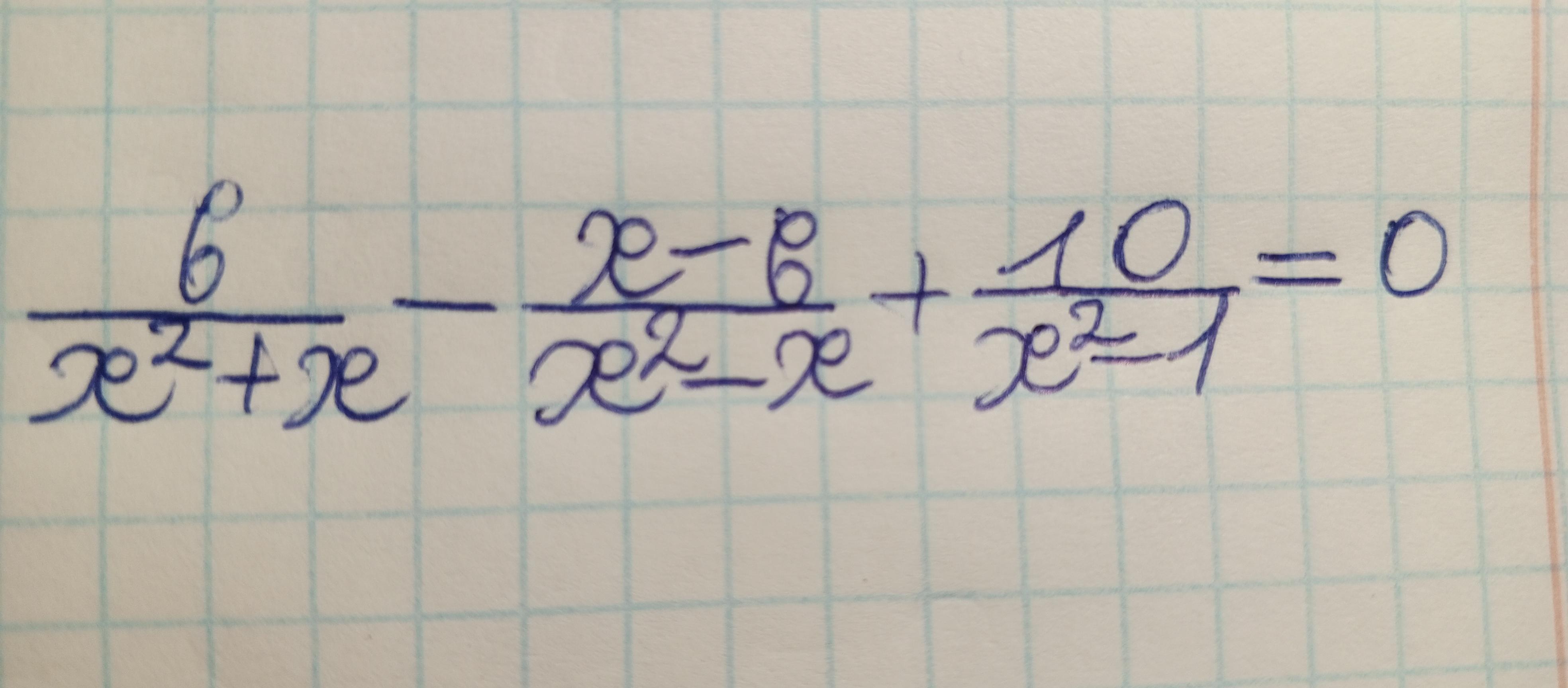
Аноним:
скину розв‘язок в інст @mathematic_89
Ответы
Ответ дал:
1
ОДЗ: x(x-1)(x+1) ≠ 0
x ≠ 0 або x ≠ 1 або x ≠ -1
xЄ(-∞; -1) U (-1; 0) U (0; 1) U (1; +∞)
x = 0 або x = 21
x = 0 – сторонній корінь
Відповідь: 21.
Дякую дякую дякую щиро дякую за допомогу
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад