Question

ДАЮ 50 БАЛЛОВ, СРОЧНО!!!!
Задание 1
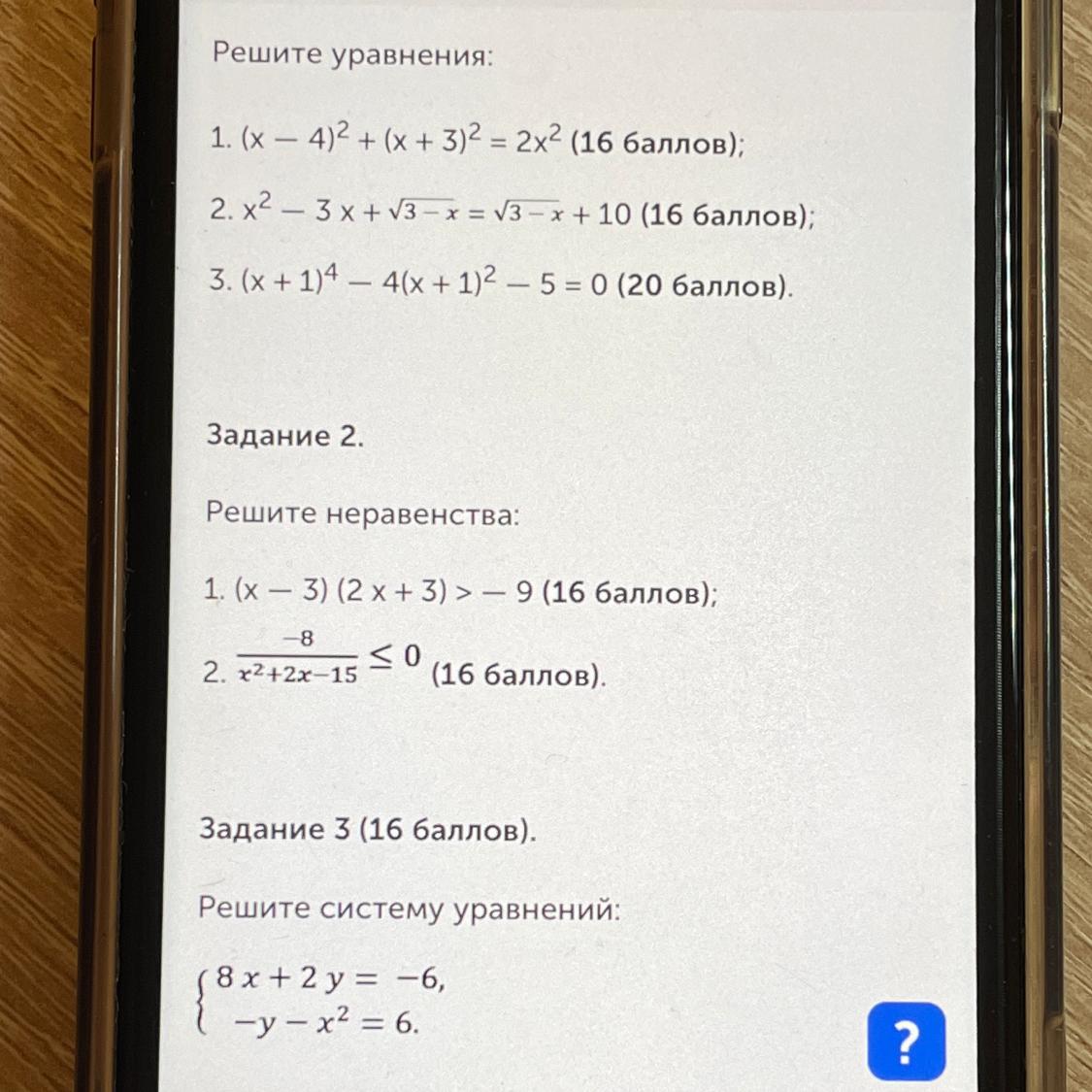
Решите уравнения:
1. (x-4)2 + (x+ 3)2 = 2x2
2. x² — 3 x + √3 - x = √3 - x + 10
3. (x + 1)4 - 4(x + 1)2 - 5 = 0
Задание 2
Решите неравенства:
1. (x-3)(2x+3)>-9
2. -8/x^2+2x-15<_0
Задание 3
Решите систему уравнений:
{8x+2y= -6
-y-x^2=6

Answer 1

Ответ: Задание 1: Решение уравнений:(x−4)2+(x+3)2=2x2(x−4)2+(x+3)2=2x2x2−8x+16+x2+6x+9=2x2x2−8x+16+x2+6x+9=2x2

2x2−2x−25=02x2−2x−25=0

x2−x−252=0x2−x−225​=0

Решення: x=1±1012Решення: x=21±101​​x2−3x+3−x=3−x+10x2−3x+3​−x=3​−x+10x2−4x+3=10x2−4x+3​=10

x2−4x+3−10=0x2−4x+3​−10=0

Решення: x=2±7Решення: x=2±7​(x+1)4−4(x+1)2−5=0(x+1)4−4(x+1)2−5=0Позначимо y=(x+1)2y=(x+1)2, тоді рівняння стає квадратним:

y2−4y−5=0y2−4y−5=0

(y−5)(y+1)=0(y−5)(y+1)=0

y=5 або y=−1y=5 або y=−1Повертаємося до xx:

Для y=5:(x+1)2=5y=5:(x+1)2=5 має два розв'язки.

Для y=−1:(x+1)2=−1y=−1:(x+1)2=−1 не має розв'язків у відповідності до властивостей квадратного кореня.Отже, рішення: x=−1±5x=−1±5​Задание 2: Решение неравенств:(x−3)(2x+3)>−9(x−3)(2x+3)>−9Розв'язок: x<−3x<−3 або x>12x>21​−8x2+2x−15≤0−x2+2x−158​≤0Розв'язок: −5≤x≤3−5≤x≤3 або x<−3x<−3 або x>5x>5Задание 3: Решение системы уравнений:{8x+2y=−6−y−x2=6{8x+2y=−6−y−x2=6​Перепишемо друге рівняння у вигляді y=−x2−6y=−x2−6 і підставимо в перше:8x+2(−x2−6)=−68x+2(−x2−6)=−6

−2x2+8x+12=0−2x2+8x+12=0

x2−4x−6=0x2−4x−6=0

x2−4x+4−10=0x2−4x+4−10=0

(x−2)2−10=0(x−2)2−10=0

(x−2)2=10(x−2)2=10Отже, рішення для xx: x=2±10x=2±10​.Підставимо значення xx назад у рівняння y=−x2−6y=−x2−6 і отримаємо відповідні значення yy.Рішення системи: {x=2±10, y=−x2−6}{x=2±10​, y=−x2−

Объяснение:

Answer 2

Задание 1: Решение уравнений

(
x
−
4
)
2
+
(
x
+
3
)
2
=
2
x
2
(x−4)
2
+(x+3)
2
=2x
2

x
2
−
8
x
+
16
+
x
2
+
6
x
+
9
=
2
x
2
x
2
−8x+16+x
2
+6x+9=2x
2

2
x
2
−
2
x
2
−
2
x
−
25
=
0
2x
2
−2x
2
−2x−25=0
−
2
x
−
25
=
0
−2x−25=0
−
2
x
=
25
−2x=25
x
=
−
25
2
x=−
2
25
​

x
2
−
3
x
+
3
−
x
=
3
−
x
+
10
x
2
−3x+
3
​
−x=
3
​
−x+10
x
2
−
4
x
+
3
=
10
x
2
−4x+
3
​
=10
x
2
−
4
x
+
3
−
10
=
0
x
2
−4x+
3
​
−10=0
Здійснимо коренівне визначення коефіцієнтів.
D
=
(
−
4
)
2
−
4
(
3
−
10
)
D=(−4)
2
−4(
3
​
−10)
D
=
16
−
4
3
+
40
D=16−4
3
​
+40
D
=
56
−
4
3
D=56−4
3
​

Рішення буде комплексними числами.
(
x
+
1
)
4
−
4
(
x
+
1
)
2
−
5
=
0
(x+1)
4
−4(x+1)
2
−5=0
Позначимо
y
=
(
x
+
1
)
2
y=(x+1)
2
:
y
2
−
4
y
−
5
=
0
y
2
−4y−5=0
Здійснимо коренівне визначення коефіцієнтів.
D
=
(
−
4
)
2
−
4
(
−
5
)
D=(−4)
2
−4(−5)
D
=
16
+
20
D=16+20
D
=
36
D=36
y
1
,
2
=
4
±
36
2
y
1,2
​
=
2
4±
36
​

​

y
1
,
2
=
4
±
6
2
y
1,2
​
=
2
4±6
​

y
1
=
5
,
y
2
=
−
1
y
1
​
=5,y
2
​
=−1
Повертаємося до
x
x:
(
x
+
1
)
2
=
5
або
(
x
+
1
)
2
=
−
1
(x+1)
2
=5або(x+1)
2
=−1
Для першого випадку:
x
+
1
=
±
5
x+1=±
5
​

x
=
−
1
±
5
x=−1±
5
​

Для другого випадку розв'язків немає, оскільки квадрат від'ємного числа не існує у межах дійсних чисел.
Задание 2: Решение неравенств

(
x
−
3
)
(
2
x
+
3
)
>
−
9
(x−3)(2x+3)>−9
Використовуємо властивості добутків:
x
2
−
3
x
−
6
x
−
9
>
−
9
x
2
−3x−6x−9>−9
x
2
−
9
x
>
0
x
2
−9x>0
x
(
x
−
9
)
>
0
x(x−9)>0
Розв'язок:
−