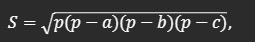Знайдіть висоту трикутника, проведену до найменшої сторони, якщо сторони трикутника дорівнюють 9, 7 і 17. Срочно даю 100 балов
Ответы
Відповідь: 39√2/7 см.
Пояснення:
У ΔАВС АВ = 7 ; ВС = 9 ; АС = 13 . Із наслідка з теореми косинусів
визначили , що ∠АВС - тупий . Тому висота СН опущена на
продовження до найменшої сторони АВ .
Нехай ВН = х см , тоді АН = ( х + 7 ) см . За теоремою Піфагора
1) із прямок. ΔВСН : СН² = 9² - х² ;
2) із прямок. ΔАСН : СН² = 13² - ( 7 + х )² . Прирівняємо праві част.
13² - ( 7 + х )² = 9² - х² ; після перетворень і спрощень маємо :
14х = 39 ;
х = 2 11/14 см ; тоді висота СН із рівності 1)
СН = √( 9²- ( 2 11/14 )² ) = √( 12168/196 ) = 39√2/7 ( см ) ; СН = 39√2/7 см.
За даними умови, найменша сторона трикутника дорівнює 7. Щоб знайти висоту, проведену до цієї сторони, нам потрібно знати площу трикутника. За формулою Герона, площа трикутника дорівнює: (фото)
де p - півпериметр трикутника, а a, b, c - його сторони. Підставляючи дані значення, отримуємо:
p = 9 + 7 + 17\2 = 16.5,
S = корень16.5(16.5 - 9)(16.5 - 7)(16.5 - 17)} =(приблизно) 21.21
Тепер, знаючи площу трикутника і довжину найменшої сторони, ми можемо знайти висоту за формулою:
h = 2S\a,
де h - висота, a - найменша сторона. Підставляючи значення, отримуємо:
h = 2*21.21\7=(приблизно) 6.06.
Отже, висота трикутника, проведена до найменшої сторони, дорівнює приблизно 6.06.