ТЕРМІНОВО ПОТРІБНА ДОПОМОГА!
Розв'язати рівняння з застосуванням законів комбінаторики.
Приложения:

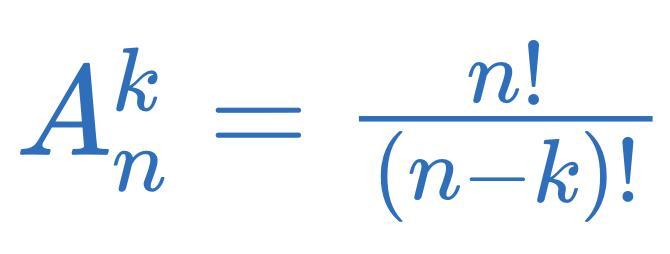
Ответы
Ответ дал:
2
Ответ:
х = 10
Объяснение:
x₂ = -5 не подходит по смыслу, тогда наш ответ
х₁ = 10
Проверим
что и требовалось получить
rsofpg2007:
Огромнейшее тебе спасибо! Я долго пытался понять где я застреваю но твое пояснение мне раскрыло глаза. Спасибо тебе! Дай Бог тебе здоровья!
пожалуйста -)) обращайтесь -))
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад