Неперервна випадкова величина X заданої функції розподілу F(x) . Визначте: а) математичне сподівання випадкової величини Х; б) дисперсію випадкової величини Х, в)ймовірність того, що випадкова величина Х матиме значення, що належить інтервалу (α,β). α=0,5 β=4,5
Приложения:
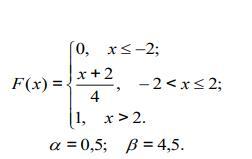
Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:Для обчислення математичного сподівання \(\mu\) неперервної випадкової величини \(X\) за функцією розподілу \(F(x)\) використовується наступна формула:
\(\mu = \int_{-\infty}^{\infty} x \cdot f(x) \,dx\),
де \(f(x)\) - щільність ймовірності.
Для обчислення дисперсії \(\sigma^2\) використовується формула:
\(\sigma^2 = \int_{-\infty}^{\infty} (x - \mu)^2 \cdot f(x) \,dx\).
Щоб знайти ймовірність того, що випадкова величина \(X\) потрапить у проміжок \((\alpha, \beta)\), можна скористатися формулою:
\(P(\alpha < X < \beta) = F(\beta) - F(\alpha)\).
На жаль, без конкретної функції розподілу \(F(x)\), я не можу обчислити ці значення. Якщо у вас є конкретна функція розподілу \(F(x)\), я зможу допомогти з цими розрахунками.
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад