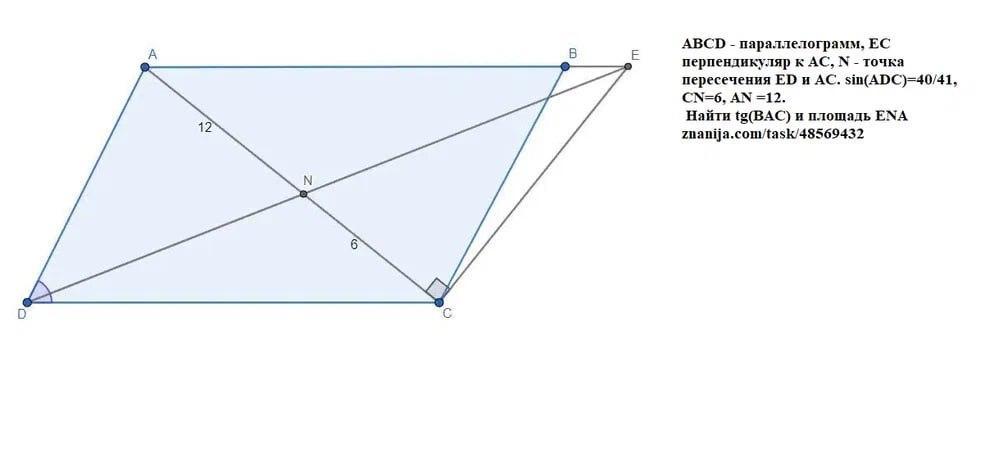
ABCD - параллелограмм, EC- перпендикуляр к АС, N-точка пересечения ED и AC,
sin(ADC)=40/41, CN=6, AN =12.
Найти tg(ВАС) и площадь треугольника ENA.
ПОЖАЛУЙСТА помогите быстро.
Актуально до 17.00 сегодня,23.11.2023
Ответы
AND~CNF, AD/CF=12/6=2/1
=> BF=AD/2 => BF -средняя линия AED
=> BC - медиана AEC => AB=BC
=> ABCD -ромб
Пусть AH=40, AD=41, тогда по т Пифагора
DH =√(AD^2-AH^2) =9 ; HC=32
tg(BAC) =tg(ACH)=AH/HC=40/32 =5/4
EC =AC tg(BAC) =18*5/4
S(AEN) =1/2 AN*EC =12*18*5/4*2 =135

Ответ:
tg∠BAC = 5/4; S(ENA) = 135
Объяснение:
ABCD - параллелограмм, EC- перпендикуляр к АС, N-точка пересечения ED и AC, sin(ADC)=40/41, CN=6, AN =12.
Найти tg(ВАС) и площадь треугольника ENA.
Дано: АВСD - параллелограмм;
ЕС ⊥ АС;
sin(ADC) = 40/41;
CN=6, AN =12
Найти: tg∠BAC; S(ENA)
Решение:
Рассмотрим ΔDNC и ΔENA;
∠DCA = ∠CAE (накрест лежащие при AE || DC и секущей АС)
∠DNC = ∠ANE (вертикальные)
⇒ ΔDNC ~ ΔENA
Запишем отношение сходственных сторон:
⇒ AE = 2DC
Рассмотрим ΔАСЕ - прямоугольный.
СВ - медиана.
- Медиана, проведенная из вершины прямого угла к гипотенузе, равна ее половине.
⇒ СВ = АВ
⇒ ABCD - ромб.
Проведем высоту АТ.
- Синус угла - отношение противолежащего катета к гипотенузе.
Из ΔDAT:
Пусть АТ = 40х, тогда AD = 41x
По теореме Пифагора:
DT² = DA² - AT² = 1681x² - 1600x² = 81x² ⇒ DT = 9x
TC = 41x - 9x = 32x
- Тангенс угла - отношение противолежащего катета к прилежащему.
Из ΔТАС:
∠DCA = ∠BAC ⇒ tg∠BAC = 5/4
- Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам.
Из ΔDOC:
OC = 18 : 2 = 9
Рассмотрим DBEC.
DC || BE; DC = BE
⇒ DBEC - параллелограмм.
- Противоположные стороны параллелограмма равны.
⇒ DB = CE = 45/2
- Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.
