Question

ПОМОГИТЕ ПОЖАЛУЙСТА,НАЙТИ ПЛОЩАДЬ ТРАПЕЦИИ,БЕЗ ТЕОРЕМЫ ПИФАГОРА

Answer 1

Ответ:

96 квадратных единиц.

Объяснение:

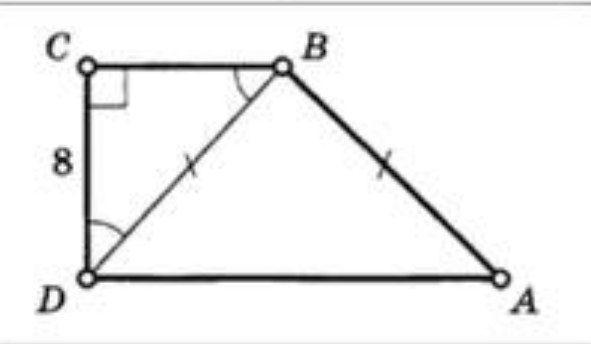
1. В ∆ BCD по условию ∠ 1 = ∠ 2, тогда по признаку ∆ ВСD равнобедренный, и ВС = СD.

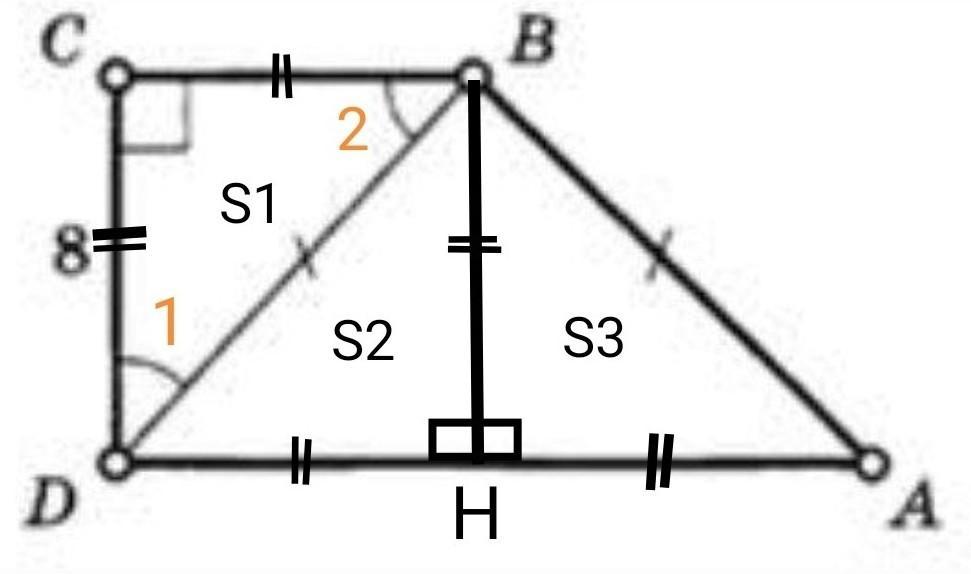
2. Пусть ВН ⊥ AD, H є АD, тогда DCBH - прямоугольник, а т.к. ВС = СD, то DCBH - квадрат

S кв. = DC² = 8² = 64.

3. ∆ DBC = ∆ DBH = ∆ ABH по гипотенузе и катету

(DB = AB по условию, СВ = ВН как стороны квадрата), тогда и их площади будут равными,

S1 = S2 = S3 = 64 : 2 = 32.

4. S трапеции = S1 + S2 + S3 = 32 • 3 = 96

Ответ: 96.

Если изучена теорема о площади трапеции, то

S = (BC + AD)/2 • BH = (8 + 16)/2 • 8 = 12 • 8 = 96.