Ответы
Ответ:
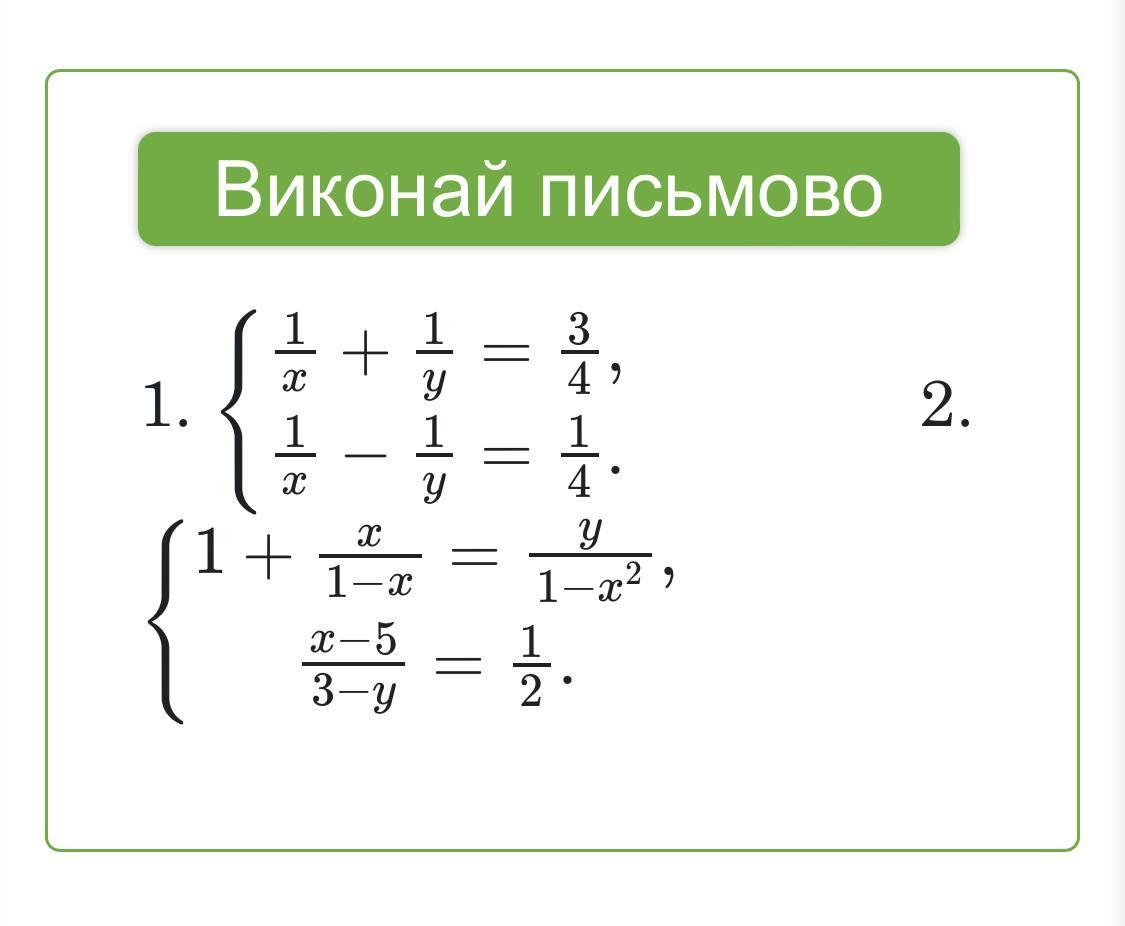
Решить систему уравнений:
1/x + 1/y = 3/4
1/x - 1/y = 1/4
Сложить уравнения:
1/x + 1/x + 1/y-1/y = 3/4 + 1/4 2/x = 1 x = 2;
Подставить значение х в любое из уравнений и вычислить у: 1/2 + 1/y = 3/4 2y + 4 = 3y 2y - 3y = -4
-y = -4
y = 4.
2 Решение системы уравнений (2; 4).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений
Объяснение:
Решить систему уравнений:
1 + x/(1-x) =y/(1 - x²) (x - 5)/(3 - y) = 1/2
Упростить первое уравнение:
(1 - x²) = (1 - x)(1+x)
Умножить уравнение (все части) на это выражение, чтобы избавиться от дроби: (1-x)(1+x) +x*(1 + x) = y
1 - x² + x + x² = y
1 + x = y;
Упростить второе уравнение: (x-5)/(3 - y) = 1/2
Умножить уравнение (все части) на 2(3-
у), чтобы избавиться от дроби: 2*(x-5) = 3-y 2x - 10 = 3-у 2x + y = 13;
Получили упрощенную систему
уравнений: 1 + x = y; 2x + y = 13;
x =y-1
2(y - 1) + y = 13
2y - 2 + y = 13
3y = 15
y = 5;
x =y-1
x = 4.
Це все, що я можу дати
Відповідь:
Пояснення:
розв'язання завдання додаю