Ответы
Ответ:
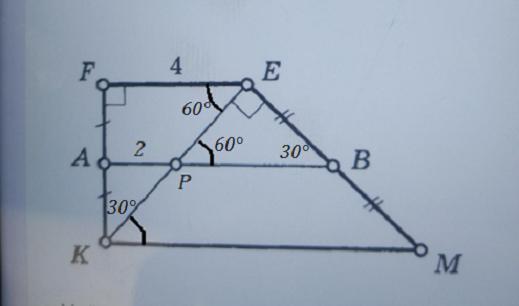
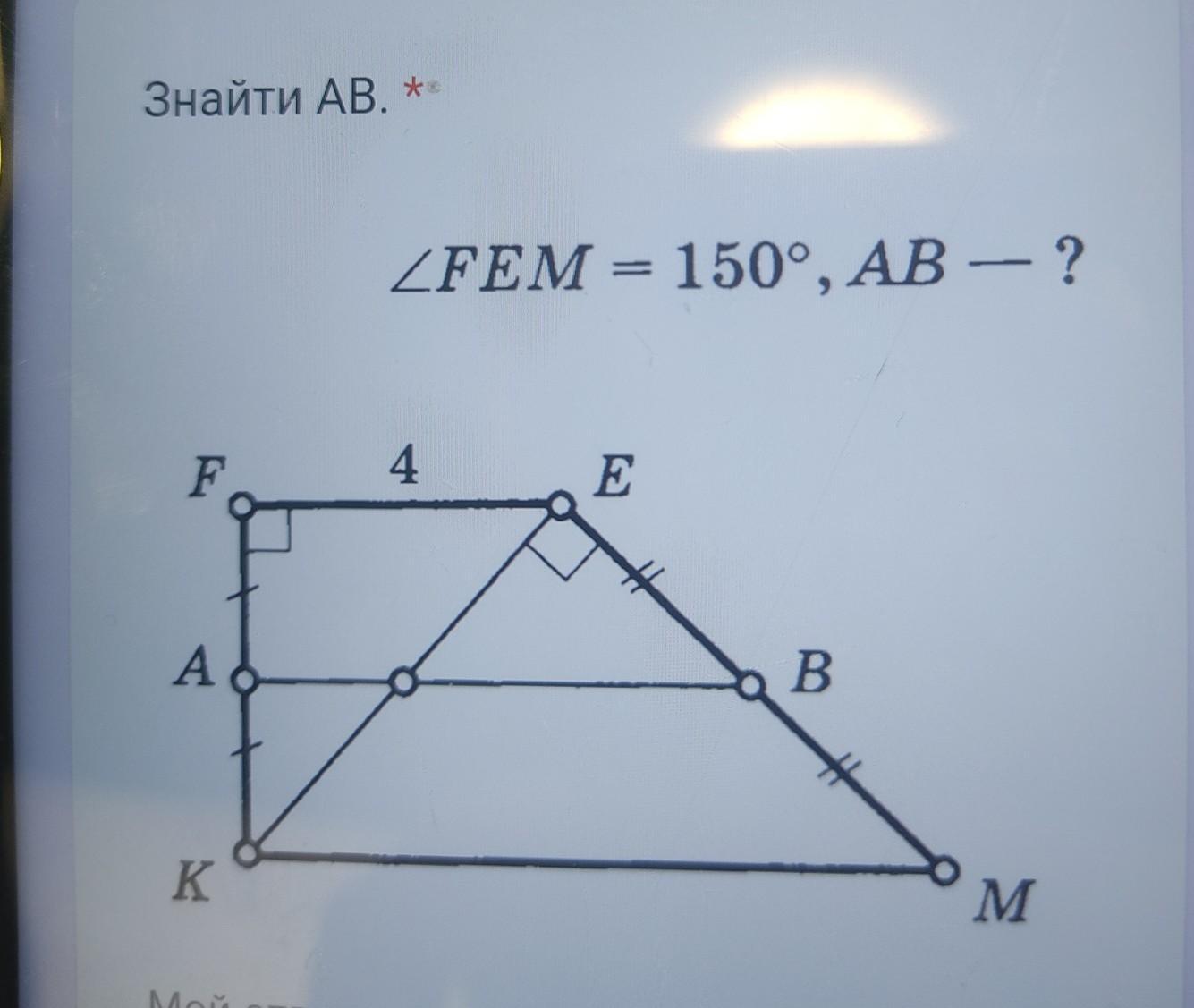
Задана прямоугольная трапеция KFEM , ∠F=∠K=90° , ∠KEM = 90° ,
EF = 4 , ∠EFM = 150° ,
AK = AF , ВЕ = ВМ ⇒ АВ = средняя линия трапеции .
Значит и диагональ КЕ средняя линия трапеции АВ делит пополам в точке Р .
Тогда АР - средняя линия треугольника KFE .
Она равна половине EF , то есть АР = 4 ; 2 = 2 .
Найдём ∠KEF = ∠FEM - ∠KEM = 150°-90°=60° .
Из прямоугольного Δ КFЕ найдём ∠FKE = 90° - 60° = 30° .
Катет ЕF лежит против угла в 30° , значит ЕF равен половине гипотенузы КE ⇒ КE = 2 · EF = 2 · 4 = 8 .
В точке Р диагональ КЕ делится пополам и РЕ = 8 : 2 = 4 .
Так как средняя линия трапеции параллельна её основаниям , то из того что EF || АВ , следует что ∠FЕР = ∠ЕPB = 60° как внутренние накрест лежащие углы ( секущая - КЕ ) .
Рассмотрим Δ РЕВ . Он прямоугольный , его катет РЕ = 4 ,
∠ЕPB = 60° , тогда ∠PBЕ = 30° и гипотенуза РВ равна удвоенному катету РЕ , то есть РВ = 2 · 4 = 8 .
АВ = АР + РВ = 2 + 8 = 10