Question

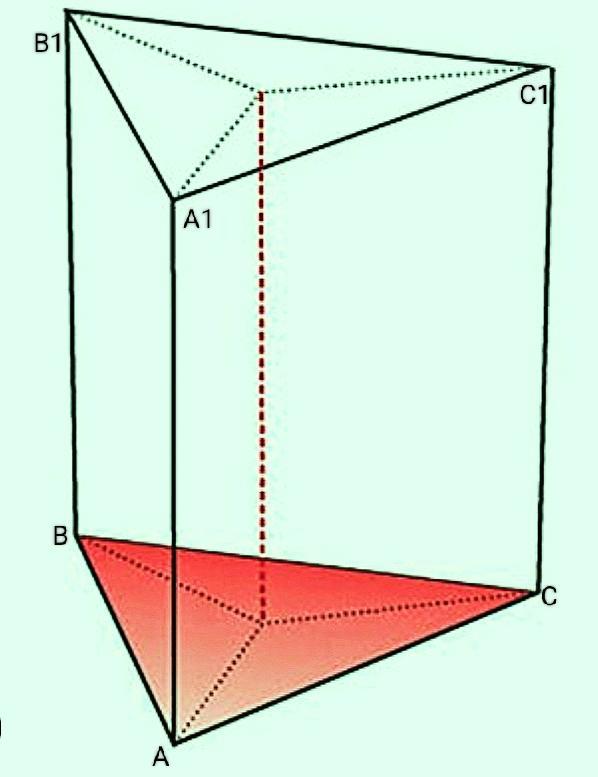
Знайти повну поверхню прямої призми.Основа призми:Трикутник зі сторонами 20 см, 21 см, 29 см .Висота призми 9 см.К задаче оформить рисунок

Answer 1

Ответ:

1050см²

Объяснение:

• Площа бічної й поверхні прямої призми знаходиться за формулою:

S = P * h

де:

Р - периметр основи;

h - висота призми;

• Знайдемо периметр основи:

Р = АС + АВ+ ВС

де:

АС, АВ, ВС - сторони трикутника;

Р = 20 + 21 + 29 = 70см

Підставимо знайдений периметр і висоту у формулу бічної поверхні та обчислимо:

S1 = 70 * 9 = 630см²

• Повна поверхня призми складається з бокової поверхні та двох основ:

S2 = 2 * S(осн)

• Площа поверхні основи трикутника можна знайти за формулою Герона, яка враховує довжини всіх сторін трикутника:

p = P / 2 = 70 / 2 = 35см

де:

р - напівпериметр;

S(осн) = √(р(р - АС)(р - АВ)(р - ВС))

= √(35(35 - 20)(35 - 21)(35 - 29)) =

= 210см²

• Площа двох основ:

S2 = 2 * 210 = 420см²

Повна поверхня призми - це сума площі основи та площі бічних поверхонь, тому:

S = S1 + S2 = 630 + 420 = 1050см²