Question

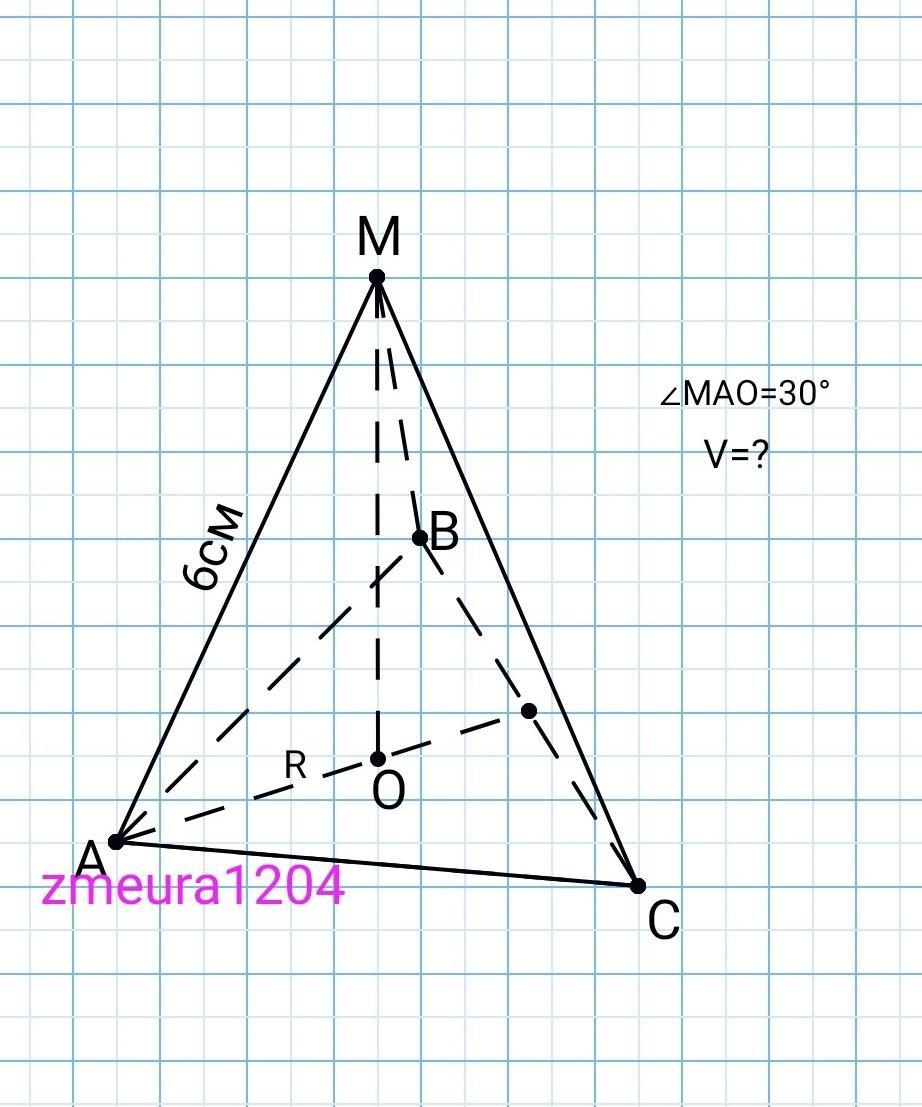
5.В правильной треугольной пирамиде боковое ребро, равно 6см, наклонено к основанию под углом 30 ^ 0 Вычислите объем пирамиды.​

Answer 1

Ответ:

Объем пирамиды равен 81√3/4см²

Объяснение:

∆MOA- прямоугольный треугольник

МО- катет проти кута 30°

МО=МА/2=6/2=3см.

АО=МО√3=3√3см (за свойством треугольника с углами 30°;60°;90°. данный катет против угла 60°)

АО=R - радиус описанной окружности.

Формула радиуса описанной окружности правильного треугольника.

R=a/√3; где а-сторона треугольника.

АВ=R√3=AO*√3=3√3*√3=9см.

So=AB²√3/4=9²√3/4=81√3/4 см²

V=⅓*So*MO=⅓*81√3/4*3=81√3/4 см³