Question

Перпендикуляр, проведений із вершини тупого кута ромба ,ділить його сторону навпіл. Периметр ромба дорівнює 36 см. Знайдіть кути ромба

Answer 1

Ответ:

Кути ромба: 30°, 150°, 30°, 150°

Объяснение:

УМОВА:

Перпендикуляр, проведений із вершини тупого кута ромба ,ділить його сторону навпіл. Периметр ромба дорівнює 36 см. Знайдіть кути ромба.

РОЗВ'ЯЗАННЯ:

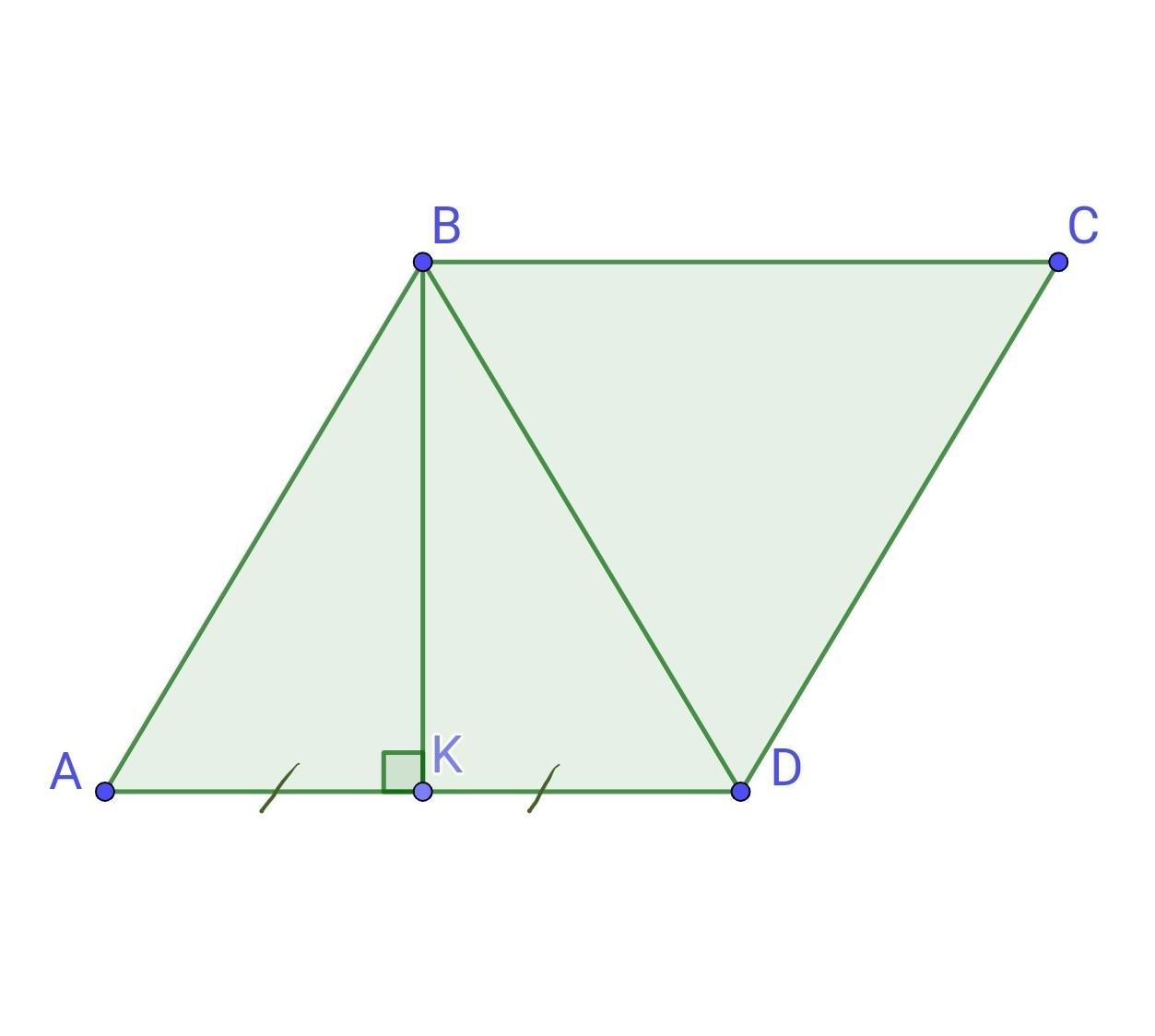
За умовою ABCD - ромб. Р(ABCD) =36 см. BK⟂AD. AK = KD.

Знайдемо ∠A, ∠B, ∠C, ∠D.

1) За означенням ромба AB = BC = CD = AD.

Тоді сторона ромба: P(ABCD) ÷ 4 = 36 ÷ 4 = 6 (см).

2) AK = KD = AD ÷ 2 = 6 ÷ 2 = 3 (см).

3) Розглянемо прямокутний трикутник АВК ( так як BK⟂AD, то ∠AKB=90°).

Катет АК = 3 см, Гіпотенуза АВ = 6 см.

За властивістю катета, який лежить навпроти кута 30°, маємо:

∠А =30°.

4) За властивістю протилежних кутів ромба маємо:

∠C = ∠A = 30°.

5) За властивістю кутів ромба, прилеглих до однієї сторони, маємо:

∠A + ∠B = 180°

∠B = ∠180° - ∠A = 180° - 30° = 150°.

6) ∠D = ∠B = 150° - за властивістю протилежних кутів ромба.

ВІДПОВІДЬ: ∠A=∠C=30°, ∠B=∠D=150°.

#SPJ1