Дано AB|ВС, ВС|BP, AB|ВР (рис. 7), BP = a, CP = b, AP=c.
Знайди AC.
розв'яжіть і оформіть терміново! будь ласочка!!!? дам 40 балів ❗
Приложения:
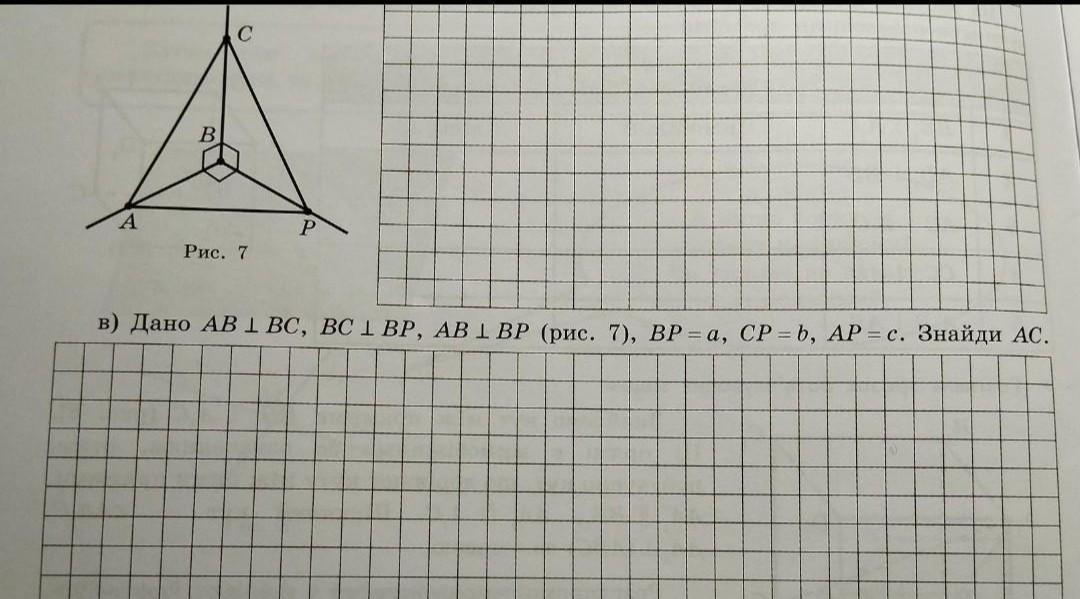
Ответы
Ответ дал:
0
За наданими даними на рисунку, ми маємо три відрізки: \(AB\), \(BC\), та \(AP\).
Для знаходження \(AC\) ми можемо скористатися теоремою стосовно внутрішньої точки на відрізку.
Теорема: Якщо точка \(P\) розташована вздовж відрізка \(AB\), то \(AP + PB = AB\).
У нашому випадку:
\(AP + PB = AB\)
\(c + a = AB\)
Також ми знаємо, що \(BC = CP + BP = b + a\).
Оскільки \(AB = BC\) (за умовою), ми можемо записати рівняння:
\(AB = BC\)
\(c + a = b + a\)
Звідси ми можемо знехтувати \(a\) з обох боків рівняння, і ми отримаємо:
\(c = b\)
Таким чином, отримали \(AC = AP + PC = c + b = 2b\).
Отже, \(AC = 2b\).
Для знаходження \(AC\) ми можемо скористатися теоремою стосовно внутрішньої точки на відрізку.
Теорема: Якщо точка \(P\) розташована вздовж відрізка \(AB\), то \(AP + PB = AB\).
У нашому випадку:
\(AP + PB = AB\)
\(c + a = AB\)
Також ми знаємо, що \(BC = CP + BP = b + a\).
Оскільки \(AB = BC\) (за умовою), ми можемо записати рівняння:
\(AB = BC\)
\(c + a = b + a\)
Звідси ми можемо знехтувати \(a\) з обох боків рівняння, і ми отримаємо:
\(c = b\)
Таким чином, отримали \(AC = AP + PC = c + b = 2b\).
Отже, \(AC = 2b\).
Ответ дал:
0
ХОРОШИСТ
За наданими даними на рисунку, ми маємо три відрізки: ((AB\), 1(BC|), та ((АР\).
Для знаходження \(AC\) ми можемо
скористатися теоремою стосовно внутрішньої точки на відрізку.
Теорема: Якщо точка ((Р)) розташована
вздовж відрізка \(AB\), то ((АР + РВ = АВ\).
У нашому випадку:
\(AP + PB = AB|)
((c + a = AB|)
Також ми знаємо, що ((ВС = СР + BP = b + al).
Оскільки ((АВ = ВС) (за умовою), ми можемо записати рівняння:
\(AB = BC|)
Nc + a = b + al)
Звідси ми можемо знехтувати \(al) з обох боків рівняння, і ми отримаємо:
1(c = bl)
Таким чином, отримали \(AC = AP + PC = с + b
=2b\).
Отже, ((АС = 2b\).
За наданими даними на рисунку, ми маємо три відрізки: ((AB\), 1(BC|), та ((АР\).
Для знаходження \(AC\) ми можемо
скористатися теоремою стосовно внутрішньої точки на відрізку.
Теорема: Якщо точка ((Р)) розташована
вздовж відрізка \(AB\), то ((АР + РВ = АВ\).
У нашому випадку:
\(AP + PB = AB|)
((c + a = AB|)
Також ми знаємо, що ((ВС = СР + BP = b + al).
Оскільки ((АВ = ВС) (за умовою), ми можемо записати рівняння:
\(AB = BC|)
Nc + a = b + al)
Звідси ми можемо знехтувати \(al) з обох боків рівняння, і ми отримаємо:
1(c = bl)
Таким чином, отримали \(AC = AP + PC = с + b
=2b\).
Отже, ((АС = 2b\).
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
8 лет назад