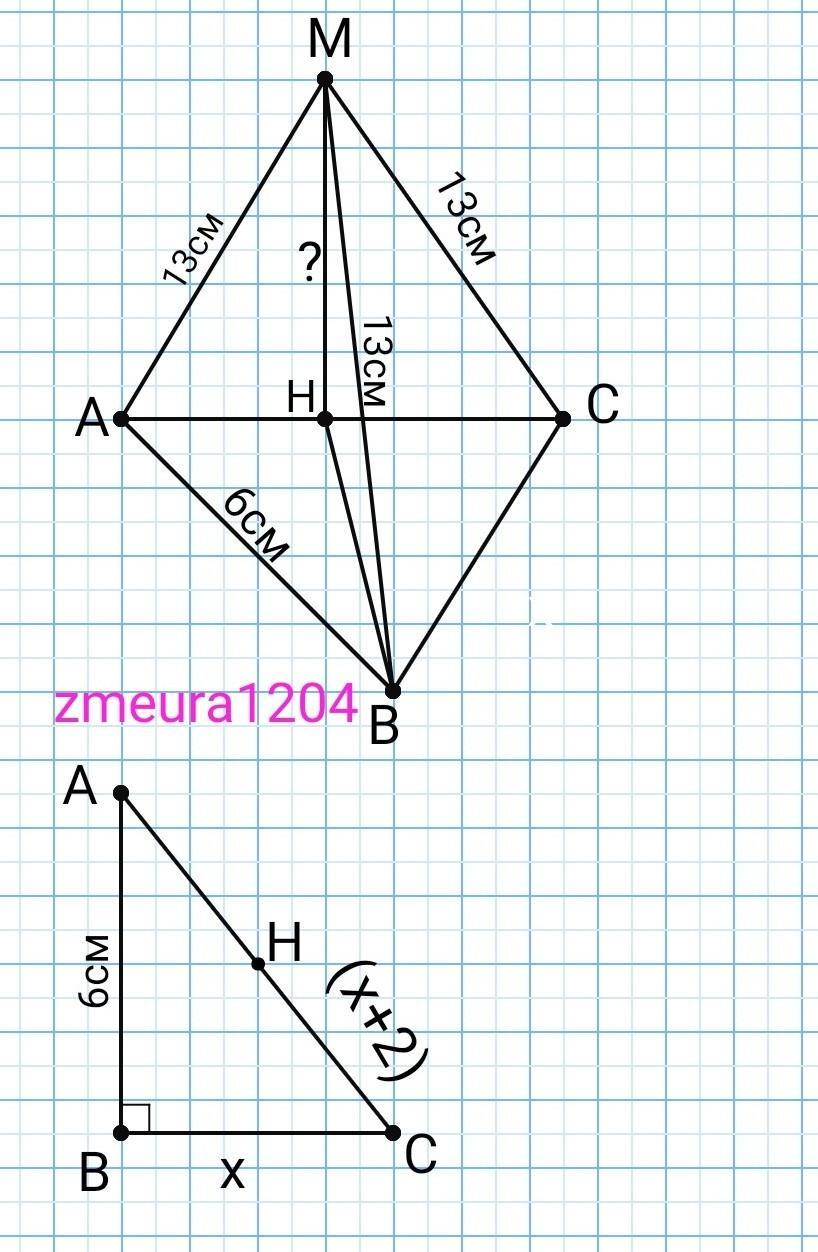
Один із катетів прямокутного трикутника дорівнює 6 см, а другий — на 2 см коротший за гіпотенузу. Точка, що не лежить у площині трикутника, віддалена від кожної з його вершин на 13 см. Знайди відстань від даної точки до площини трикутника.
Ответы
Ответ дал:
5
Ответ:
Відстань від точки до площини трикутника дорівнює 12см
Объяснение:
АВ=6см
ВС=х см
АС=(х+2)см
∆ABC- прямокутний трикутник.
За теоремою Піфагора:
АС²=АВ²+ВС²
Складаємо рівняння
6²+х²=(х+2)²
36+х²=х²+4х+4
4х=36-4
х=32/4
х=8см. ВС
АС=8+2=10см
АН=НС=ВН=R радіуси описаного кола
ВН- медіана прямокутного трикутника, дорівнює половині гіпотенузи.
AH=AC/2=10/2=5см
∆АНМ- прямокутний трикутник.
Теорема Піфагора:
НМ=√(АМ²-АН²)=√(13²-5²)=12см
Приложения:
zmeura1204:
Що не зрозуміло?
zmeura1204, здрастуйте! Допоможіть, будь ласка, з геометрією, якщо не складно. Буду вам дуже вдячна!
питання у профілі
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад