Question

2. Побудуйте графік функції g(x)=x^2+4x+3 за графіком знайдіть:
1) g(1), g(-3);
2) нулi функції;
3) g(x)>0, g(x)
4) проміжки зростання та проміжки спадання функції.

Answer 1

Ответ:

в объяснении

Объяснение:

Строим график функции.

Для этого преобразуем функцию.

$\displaystyle g(x) = x^2+4x+3=(x^2+4x+4)-4+3=(x+2)^2-1$

Теперь берем за основу известную функцию у = x².

Согласно правилам смещения графиков, смещаем функцию на -2 (на 2 единицы влево) по оси ОХ и на -1 (на 1 единицу вниз) по оси OY.

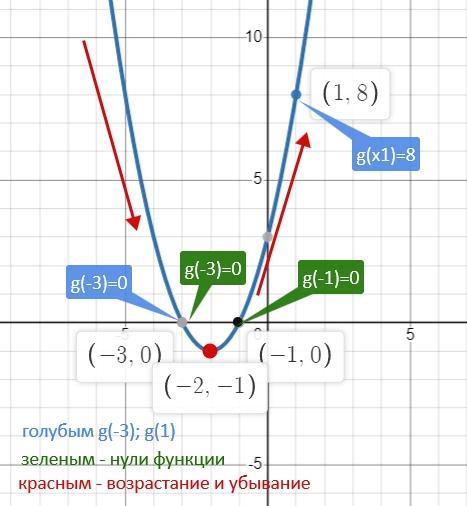
1). g(1) = 8;  g(-3) = 0

2). x₁ = -3;  x₂ = -1

3) g(x) > 0   x ∈ (-∞; -3) ∪ (-1; +∞)

g(x) < 0    x ∈ (-3; -1)

4) функция возрастает х ∈ [-2; +∞)

функция убывает x ∈ (-∞; -2]