здравствуйте, помогите пожалуйста решить задачу, кто нибудь знает как решить эту задачу , найти определител , актуально 10ч
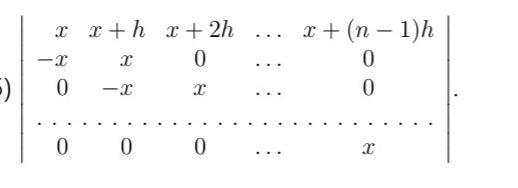
Ответы
Ответ:
Объяснение:
У меня нет времени рисовать определители, поэтому не обижайтесь, если решение не очень легко будет понять. Вычислим непосредственно определители при нескольких малых n.
Если гипотезу относительно формулы в общем виде выдвинуть не удается, можно посчитать определитель при n=4 (разложив, например определитель по последнему столбцу). Выписываю сразу результат (мы им будем пользоваться только для выдвижения гипотезы):
Выдвигаем гипотезу: определитель n-го порядка есть сумма двух слагаемых; первое слагаемое есть n- я степень икса, умноженная на n, а второе - (n-1)-я степень икса, умноженная на h и на некоторое число, которое, возможно, есть сумма целых чисел от нуля до (n-1), то есть равно Итак, вот наша гипотеза:
Подставляя (не доверяя себе) вместо n значения 1, 2, 3, 4, убеждаемся, что при этих n формула дает правильный ответ.
Чтобы доказать формулу в общем виде, воспользуемся методом математической индукции. Для малых n формулу мы проверили, остается только предположить, что она верна при некотором n и доказать ее справедливость при (n+1). Иными словами, мы должны доказать, что
Для этого разложим определитель по последнему столбцу. В нем только два ненулевых элемента, поэтому
Здесь - это определитель n-го порядка, у которого все элементы равны нулю, кроме элементов на главной диагонали - все они равны (-x), и элементов над главной диагональю - все они равны x. По любому это верхнетреугольная матрица, и определитель равен произведению чисел на главной диагонали, то есть
Поэтому
Таким образом, наша гипотеза подтвердилась, и задача полностью решена.