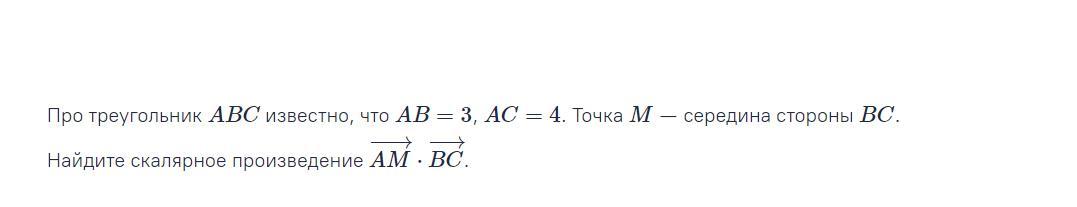Ответы
Ответ дал:
1
Ответ:
3,5.
Объяснение:
Замечание. То, что вектор, идущий по медиане треугольника, равен полусумме векторов, идущих по сторонам, следует из того, что медиана треугольника - это половина диагонали параллелограмма, построенного на векторах, идущих по сторонам треугольника.
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад