3. В геометрической прогрессин (b) прогрессии. известно b1 = 5, q = -2. Запишите первые пять членов
Приложения:
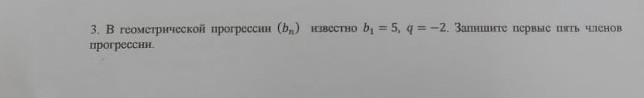
Ответы
Ответ дал:
0
Ответ:
Объяснение:
Для нахождения первых пяти членов геометрической прогрессии нужно использовать формулу:
bn = b1 * q^(n-1),
где:
bn - n-й член прогрессии,
b1 - первый член прогрессии,
q - знаменатель прогрессии,
n - номер члена прогрессии.
Исходя из условия, где b1 = 5 и q = -2, мы можем подставить эти значения в формулу и вычислить первые пять членов:
b1 = 5
b2 = b1 * q = 5 * (-2) = -10
b3 = b1 * q^2 = 5 * (-2)^2 = -20
b4 = b1 * q^3 = 5 * (-2)^3 = -40
b5 = b1 * q^4 = 5 * (-2)^4 = -80
Таким образом, первые пять членов геометрической прогрессии с b1 = 5 и q = -2 будут:
5, -10, -20, -40, -80.
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад