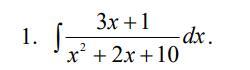Ответы
Ответ дал:
1
Ответ:
в объяснении
Объяснение:
решим первый интеграл
решим второй интеграл
ответ
fctdgsygfdhngfxzgsac:
спасибо большое)
если еще будет возможность помочь, то у меня в профиле есть еще 2 вопроса
https://znanija.com/task/54275064
https://znanija.com/task/54275684
https://znanija.com/task/54275064
https://znanija.com/task/54275684
пожалуйста -))
Вас заинтересует
1 год назад
1 год назад
1 год назад
8 лет назад