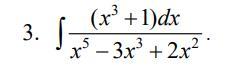Ответы
Ответ дал:
2
Ответ:
Разложим правильную дробь на сумму простейших дробей .
Приравняем коэффициенты при старшей степени х³ :
Вычислим интеграл .
fctdgsygfdhngfxzgsac:
спасибо большое)
Добрый день
Не могли бы вы мне помочь с Алгеброй?
https://znanija.com/task/54274983 (здесь нужно решить 2 уравнения)
https://znanija.com/task/54275010 (здесь нужно найти область определения функции)
Не могли бы вы мне помочь с Алгеброй?
https://znanija.com/task/54274983 (здесь нужно решить 2 уравнения)
https://znanija.com/task/54275010 (здесь нужно найти область определения функции)
Вас заинтересует
1 год назад
1 год назад
2 года назад
8 лет назад
8 лет назад