Решите, пожалуйста 4, даю 100 баллов
Приложения:

NNNLLL54:
1а ответ неверен , надо х=3П/4+2Пk , kЭZ
х= +-3П/4+2Пk , kЭZ
Ответы
Ответ дал:
1
Ответ:
4) Решить тригонометрическое неравенство .
Приложения:
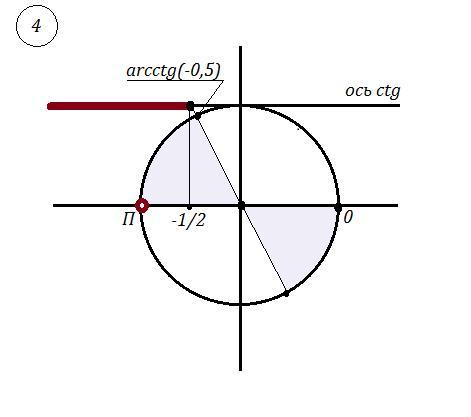

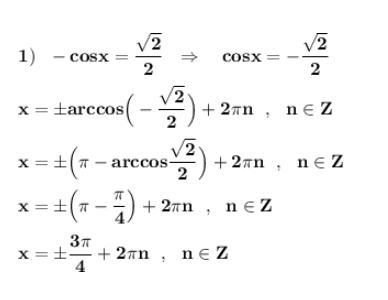
см.
Добрый день
Не могли бы вы мне помочь с Алгеброй?
https://znanija.com/task/54274983 (здесь нужно решить 2 уравнения)
https://znanija.com/task/54275010 (здесь нужно найти область определения функции)
Не могли бы вы мне помочь с Алгеброй?
https://znanija.com/task/54274983 (здесь нужно решить 2 уравнения)
https://znanija.com/task/54275010 (здесь нужно найти область определения функции)
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад