16.2. В геометрической прогрессии (bn ) найдите q и Sn, если: b = 90, bn = 3 1/3, n = 4;
Приложения:
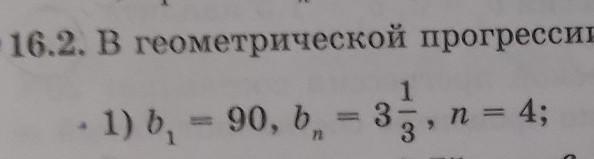
Ответы
Ответ дал:
1
Ответ:
и
Объяснение:
Информация. 1) Любой член геометрической прогрессии может быть вычислен по формуле
здесь b₁ - первый член и q - знаменатель геометрической прогрессии.
2) Сумма первых n членов геометрической прогрессии вычисляется по формуле
Решение. Так как известны b₁ = 90, и т = 4, то
Теперь вычислим S₄:
#SPJ1
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
8 лет назад