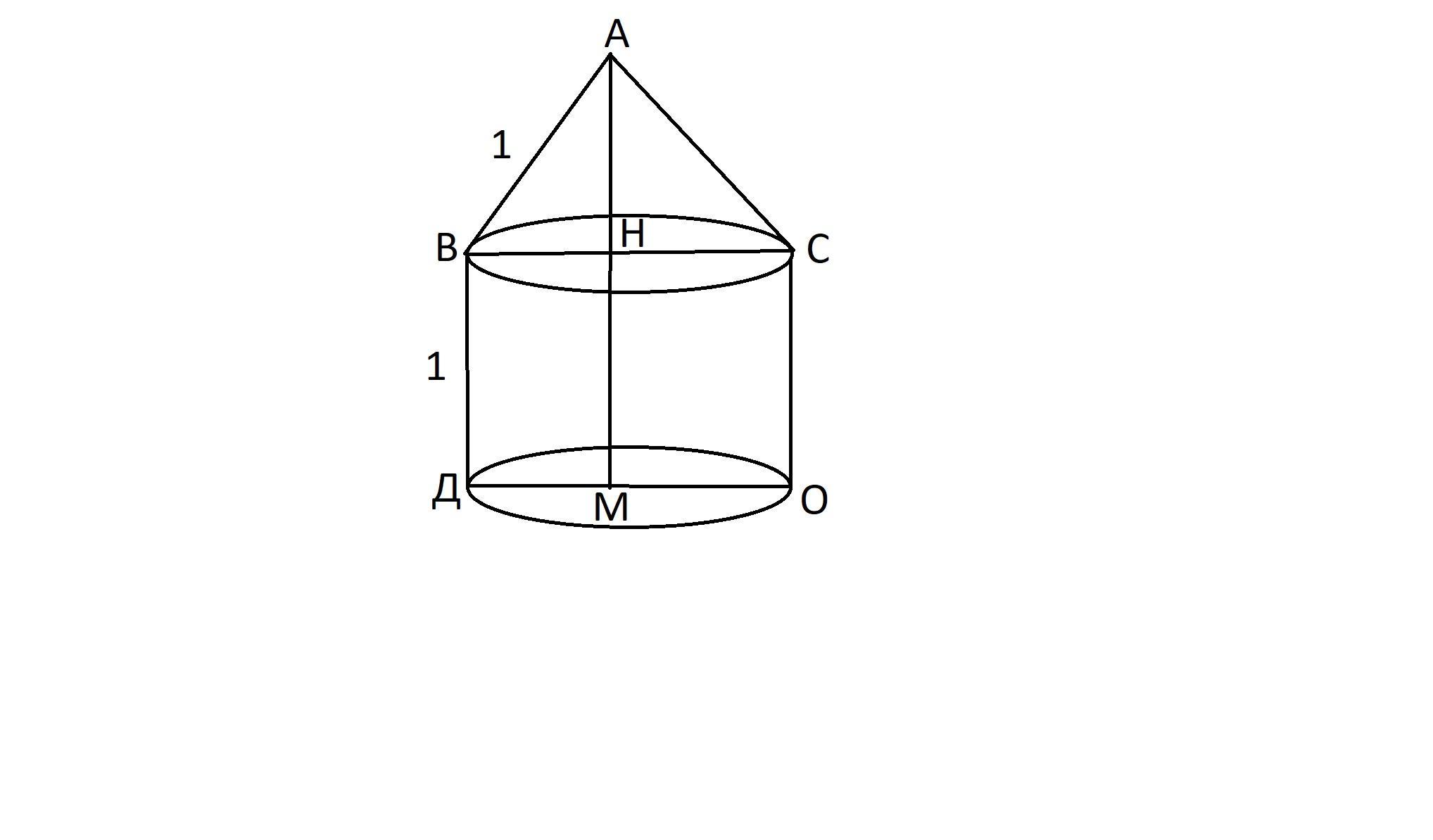
На прямий круговий циліндр із квадратним осьовим перерізом поставлено конус, осьовим перерізом якого є правильний трикутник зі стороною 1, причому, основи конуса та циліндра збіглися. Відстань від вершини конуса до нижньої основи циліндра дорівнює
Ответы
Ответ дал:
2
Ответ:
(2+√3)/2
Объяснение:
Відстань від вершини конуса до нижньої основи циліндра дорівнює:
АН+НМ
За теоремою Пыфагора: АН=√(ВА²-ВН²)
ВН=ВС/2=1/2=0,5
АН=√(1²-0,5²)=√(1-(1/4))=√(3/4)=√3/2
ВС=ВД=НМ=1
1+(√3/2=2/2+(√3/2)=(2+√3)/2
Приложения:
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад