3. Знайти об'єм тіла обертання, що обержаєшься навколо вісі ОХ
y = cos x, x = П/6 ; x = П/2
Приложения:
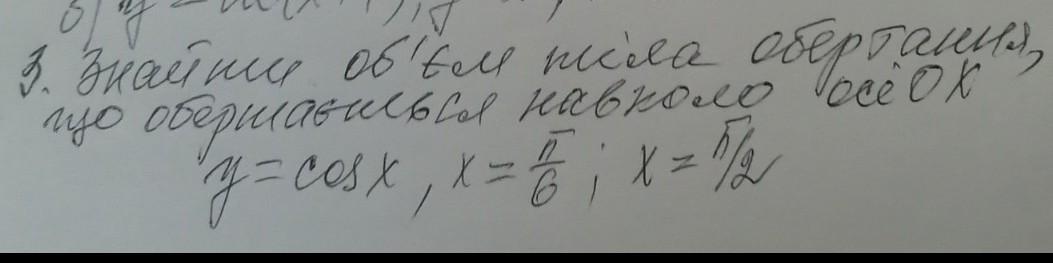
Ответы
Ответ дал:
0
Об'єм тіла обертання можна знайти за допомогою інтегралу площі поперечного перерізу, охопленого функцією обертання при обертанні навколо вісі ОХ. Формула для об'єму в даному випадку виглядає так:
\[ V = \pi \int_{a}^{b} (f(x))^2 \,dx \]
Де:
- \( f(x) \) - функція, яка обертається (у даному випадку \( y = \cos x \)),
- \( a \) і \( b \) - межі інтегрування (у даному випадку \( \frac{\pi}{6} \) і \( \frac{\pi}{2} \)).
Підставим значення і обчислимо:
\[ V = \pi \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} (\cos x)^2 \,dx \]
Цей інтеграл можна розв'язати аналітично, але для спрощення процесу використаємо символьні обчислення:
\[ V = \pi \left[ \frac{1}{2}x + \frac{1}{4}\sin(2x) \right]_{\frac{\pi}{6}}^{\frac{\pi}{2}} \]
\[ V = \pi \left[ \frac{\pi}{4} - \frac{\sqrt{3}}{8} - \left( \frac{\pi}{12} - \frac{\sqrt{3}}{24} \right) \right] \]
\[ V = \pi \left[ \frac{\pi}{6} - \frac{\sqrt{3}}{12} \right] \]
Отже, об'єм тіла обертання навколо вісі ОХ за функцією \( y = \cos x \), де \( x \) змінюється від \( \frac{\pi}{6} \) до \( \frac{\pi}{2} \), дорівнює \( \frac{\pi^2}{6} - \frac{\pi\sqrt{3}}{12} \) кубічним одиницям.
\[ V = \pi \int_{a}^{b} (f(x))^2 \,dx \]
Де:
- \( f(x) \) - функція, яка обертається (у даному випадку \( y = \cos x \)),
- \( a \) і \( b \) - межі інтегрування (у даному випадку \( \frac{\pi}{6} \) і \( \frac{\pi}{2} \)).
Підставим значення і обчислимо:
\[ V = \pi \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} (\cos x)^2 \,dx \]
Цей інтеграл можна розв'язати аналітично, але для спрощення процесу використаємо символьні обчислення:
\[ V = \pi \left[ \frac{1}{2}x + \frac{1}{4}\sin(2x) \right]_{\frac{\pi}{6}}^{\frac{\pi}{2}} \]
\[ V = \pi \left[ \frac{\pi}{4} - \frac{\sqrt{3}}{8} - \left( \frac{\pi}{12} - \frac{\sqrt{3}}{24} \right) \right] \]
\[ V = \pi \left[ \frac{\pi}{6} - \frac{\sqrt{3}}{12} \right] \]
Отже, об'єм тіла обертання навколо вісі ОХ за функцією \( y = \cos x \), де \( x \) змінюється від \( \frac{\pi}{6} \) до \( \frac{\pi}{2} \), дорівнює \( \frac{\pi^2}{6} - \frac{\pi\sqrt{3}}{12} \) кубічним одиницям.
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад