Ответы
Ответ дал:
1
Ответ:
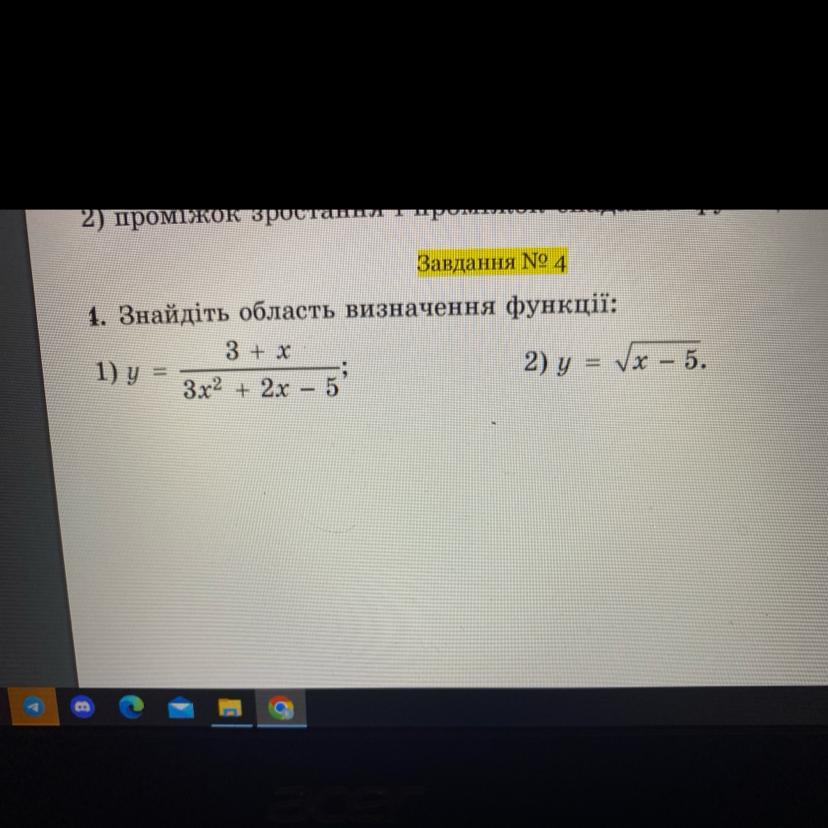
Найти область определения функции (ООФ) .
Знаменатель дроби не может быть равен 0 .
Переменная х не может быть равной ни , ни
.
ООФ: .
Подкоренное выражение должно быть неотрицательным .
ООФ: .
Приложения:

wiosjxl:
спасибо большое!
Помогите мне пожалуйста с алгеброй последнее задание в пррофиле если не сложно…
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад