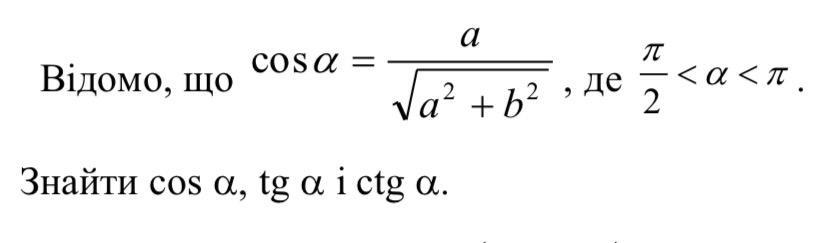Question

Срочно, даю 70 баллов

Answer 1

Ответ:

$\bf cos\alpha =\dfrac{a}{\sqrt{a^2+b^2}}\ \ ,\ \ \dfrac{\pi }{2} < \alpha < \pi$      

Так как во 2 четверти  $\bf cos\alpha < 0$  , то   $\bf \dfrac{a}{\sqrt{a^2+b^2}} < 0\ \ \Rightarrow \ \ a < 0$  .

Из тригонометрической единицы найдём

$\bf sin^2\alpha +cos^2\alpha =1\ \ \ \Rightarrow \ \ \ sin\alpha =\pm \sqrt{1-cos^2\alpha }$  

$\bf sin\alpha =\pm \sqrt{1-\dfrac{a^2}{a^2+b^2}}=\pm \sqrt{\dfrac{a^2+b^2-a^2}{a^2+b^2}}=\pm \sqrt{\dfrac{b^2}{a^2+b^2}}=\pm \dfrac{|\, b\, |}{\sqrt{a^2+b^2}}$  

Так как во 2 четверти  sinα > 0, то  $\bf sin\alpha =\dfrac{|\, b\, |}{\sqrt{a^2+b^2}}$  .

$\bf tg\alpha =\dfrac{sin\alpha }{cos\alpha }=\dfrac{|\, b\, |}{a} < 0\ \ ,\ \ \ ctg\alpha =\dfrac{cos\alpha }{sin\alpha }=\dfrac{a}{|\, b\, |} < 0$