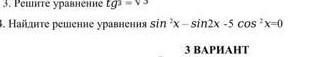Ответы
Ответ дал:
2
Объяснение:
sin²x - sin2x - 5cos²x = 0.
Мы можем заменить sin2x на 2sinx*cosx:
sin²x - 2sinx*cosx - 5cos²x = 0.
Теперь давайте преобразуем уравнение:
(sin²x - 5cos²x) - 2sinx*cosx = 0.
Мы можем использовать тригонометрическую формулу sin²x + cos²x = 1:
(1 - 6cos²x) - 2sinx*cosx = 0.
Теперь объединим подобные термины:
1 - 6cos²x - 2sinx*cosx = 0.
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад