СРОЧНООО!!!ДАЮ СТО БАЛЛОВ
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB = 1 дм, AD=2 дм, AA1= 3 дм .а) найти расстояние от точки A1 до прямой DC; б)расстояние между плоскостей А1В1С1 и МКD, М и К центр отрезок AD и CD
Ответы
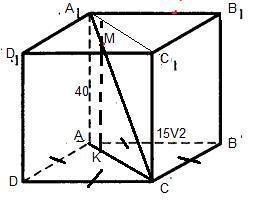
" В прямоугольном параллелепипеде АBCDA1B1C1D1, через точку М диагонали А1С,такую что А1М:МС (1:4) проведена прямая МК,параллельная АА1,где точка К принадлежит плоскасти грани АВСД. Найдите площадь треугольника МКС, если АА1=40, АВ=15 корень из 2. АВСД -квадрат".
Пояснення:
Т.к по определению прямоугольного параллелепипеда АА₁ ⊥(АВС), то МК ⊥(АВС), по условию МК||АА₁ .
Найдем из ΔАВС-прямоугольнОГО , равнобедреннОГО , АС по т. Пифагора : АС=√((15√2)²+(15√2)²)=√(2*15²*2)=30.
ΔА₁АС ≈ΔМКС по двум углам : ∠А₁АС=∠МКС =90°, ∠АА₁С=∠КМС как соответственные при МК||АА₁, А₁С-секущая.
По условию А₁М:МС=1:4 , значит к= 5/4 . По т. об отношении " В прямоугольном параллелепипеде АBCDA1B1C1D1, через точку М диагонали А1С,такую - 1площадей подобных треугольников
или . Значит S(МКС)=384 ед².