СРОЧНО ПОМОГИТЕ!!!!!!!
Тема. Треугольники
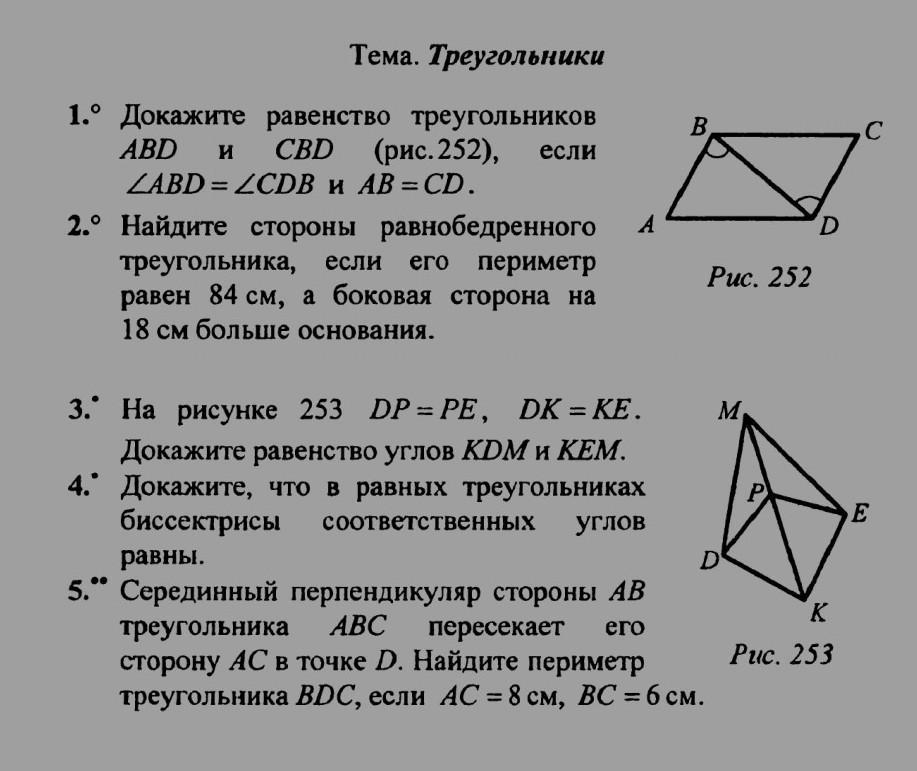
1.° Докажите равенство треугольников ABD и CBD (рис. 252), если ZABD=ZCDB и AB=CD.
2.° Найдите стороны равнобедpeHHOГO треугольника, если его периметр равен 84 см, а боковая сторона на 18 см больше основания. A 3.
4
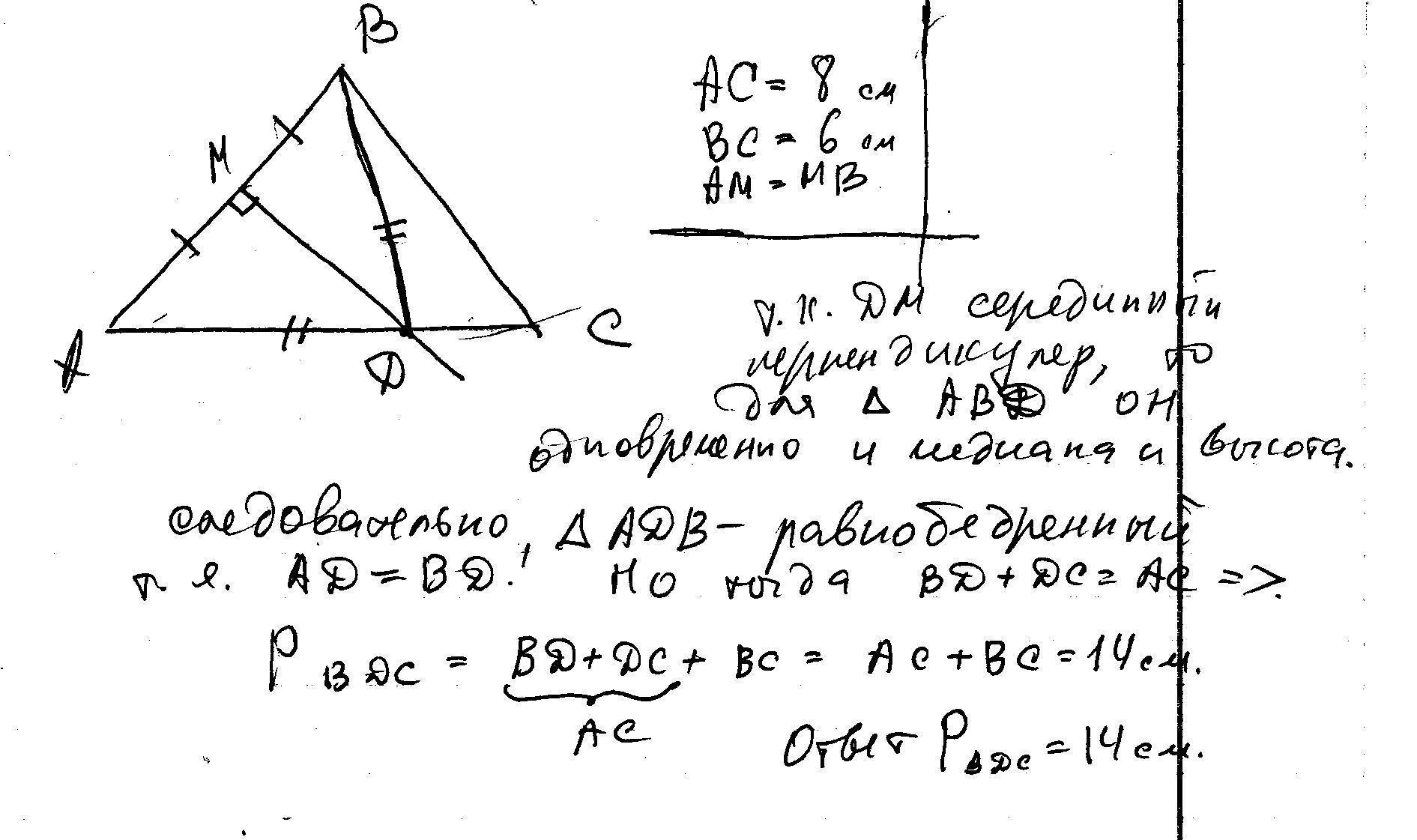
. На рисунке 253 DP=PE, DK= =KE. Докажите равенство углов KDM и KEM. Докажите, что в равных треугольниках биссектрисы соответственных углов равны. В 5. Серединный перпендикуляр стороны AB ABC пересекает его треугольника сторону АС в точке D. Найдите периметр треугольника BDC, если АС = 8 см, ВС = 6 см. Puc. 252 M D K Puc. 253 с E
Ответы
Ответ:
1) Рассмотрим ΔABD и ΔCDB
AB = CD по условию,
BD - общая сторона,
∠ABD = ∠CDB по условию ⇒
ΔABD = ΔCDB по двум равным сторонам и углу между ними (первый признак равенства треугольников)
2) Основание x и, т.к. боковые стороны больше на 18, их берем за x+18, далее состовляем уравнение и доделываем по логике (я прикрепил фото)
3) ΔPEK=ΔPDK по ССС (сторона сторона сторона) т.к. PD=PE, DK=KE, PK-общая сторона. ΔMEK=ΔMDK по СУС (сторона угол сторона) т.к. KE=KD, KM-общая сторона, ∠EKM=∠MKD⇒∠KDM=∠KEM. чтд (что и требовалось доказать)
4) Пусть в треугольник ABC равен треугольнику A1B1C1, и проведены биссектрисы AD и A1D1. Тогда углы DAB и D1A1B1 равны, кроме того, AB=A1B1, угол B равен углу B1. Значит, треугольники ABD и A1B1D1 равны по стороне и двум прилежащим к ней углам, тогда и AD=A1D1.
5) решение в скане. Задачка хитроватая, но простая.
прикрепил фото
Объяснение: