Question

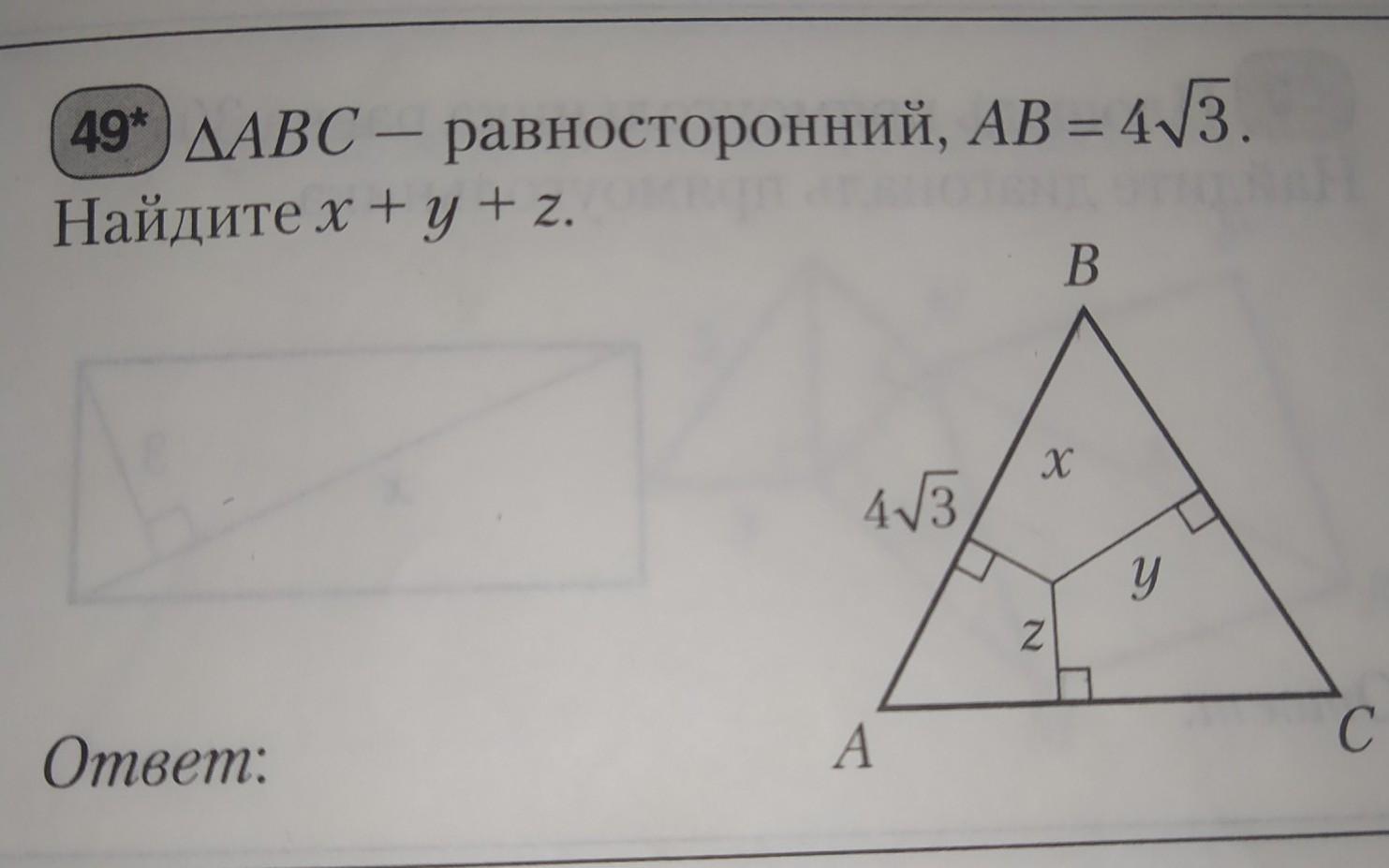
49* Треугольник ABC равносторонний, AB = 4√3. Найдите x + y + z. пожалуйста подробно​

Answer 1

Объяснение:

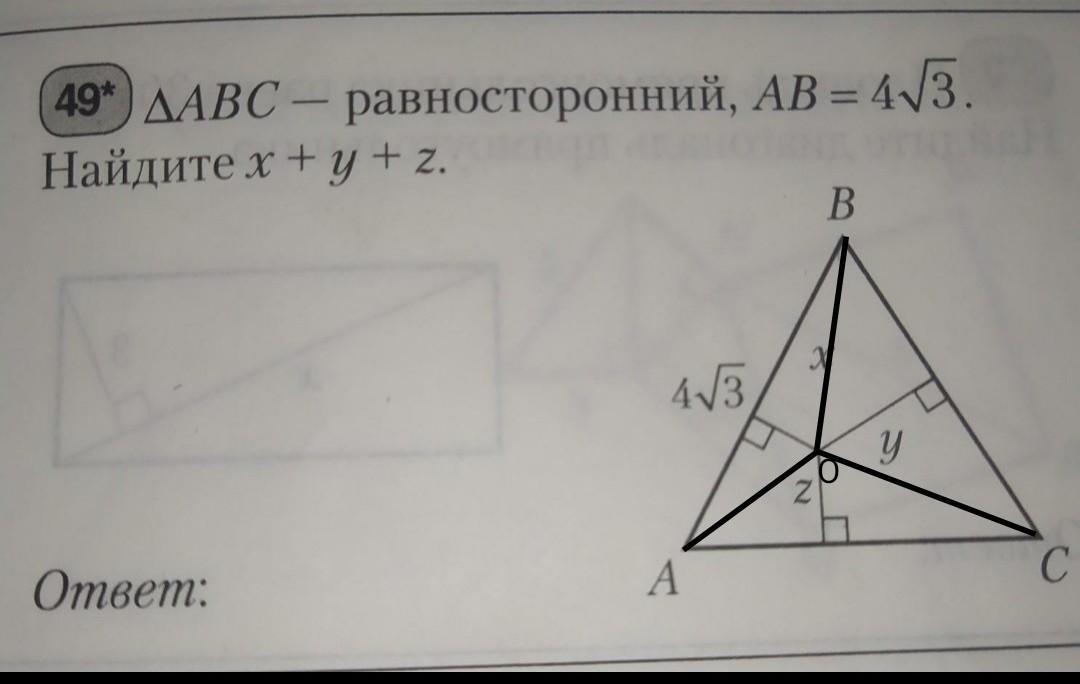
S(∆ABC)=AB²√3/4=(4√3)²√3/4=

=12√3 ед.кв.

S(∆ABO)=½*AB*x=½*4√3*x=2x√3 ед²

S(∆AOC)=½*AC*z=½*4√3*z=2z√3 ед²

S(∆BOC)=½*BC*y=½*4√3*y=2y√3 ед²

S(∆ABC)=S(∆ABO)+S(∆AOC)+S(∆BOC);

2x√3+2z√3+2y√3=12√3

2√3(x+z+y)=12√3

(x+y+z)=12√3/2√3=6 ед.

______________

Если в середине равностороннего треугольника взять точку и от нее провести перпендикуляры к сторонам, то сумма этих перпендикуляров будет равно высоте равностороннего треугольника:

Доказательство:

Обозначим сторону треугольника а.

S(∆AOB)=½*AB*x=½*a*x;

S(∆BOC)=½*BC*y=½*a*y;

S(∆AOC)=½*AC*z=½*a*z.

S(∆ABC)=½*AB*h=½*a*h; где h- высота равностороннего треугольника.

S(∆ABC)=S(∆AOB)+S(∆BOC)+S(∆AOC)

½*a*h=½*a*x+½*a*y+½*a*z

½*a*h=½*a*(x+y+z). |÷½*a

h=(x+y+z)

Что нужно было доказать.