Question

ДАЮ 80 БАЛЛОВ!! СРОЧНО!!

Діагональ рівнобічної трапеції є бісектрисою її гострого кута і ділить середню лінію трапеції на відрізки довжиною 6,5 см та 11,5 см. Знайди довжини основ трапеції. Обчисли площу трапеції

Answer 1

Ответ:

13 см    23 см   216 см²

Объяснение:

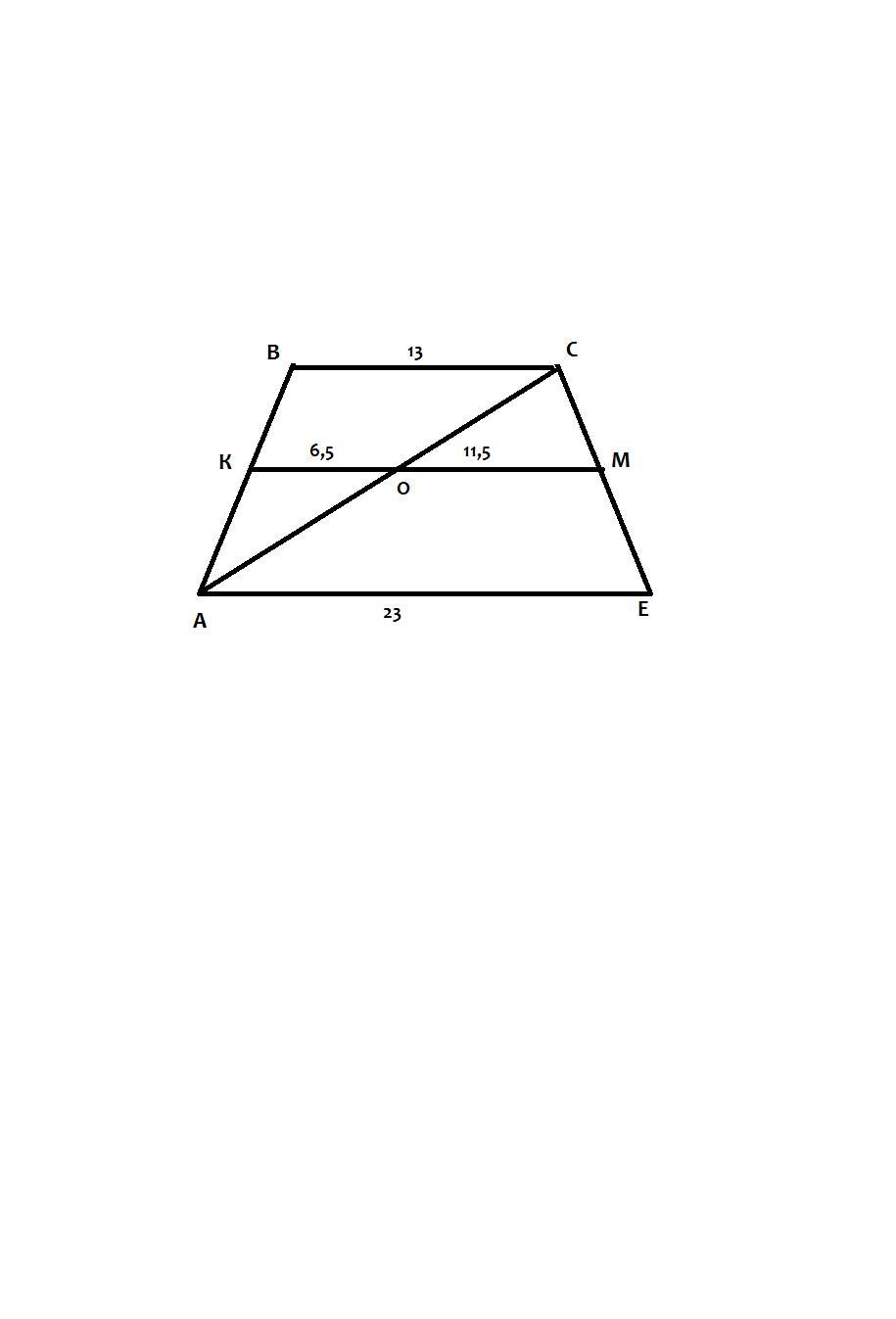
Дано: АВСЕ - трапеція, АВ=СЕ, КМ - середня лінія, КО=6,5 см, МО=11,5 см.  ВС - ?  АЕ - ? S(АВСЕ) - ?

Якщо діагональ рівнобічної трапеції є бісектрисою її гострого кута, то вона відсікає від трапеції рівнобедрений трикутник.

ΔАВС - рівнобедрений, АВ=ВС=СЕ.  КО - середня лінія,  ВС=2КО=6,5*2=13 см.;  АВ=ВС=СЕ=13 см.

ΔАСЕ, МО - середня лінія,  АЕ=2МО=11,5*2=23 см.

За формулою Герона

S(АВСЕ)=(а+b)/(b-a) * √((p-a)(p-b)(p-a-c)(p-a-d))

р - півпериметр, а - менша основа, b - більша основа, с і d - бічні сторони

S=(13+23)/(23-13) * √(18*8*5*5)=36/10 * 60 = 216 см²