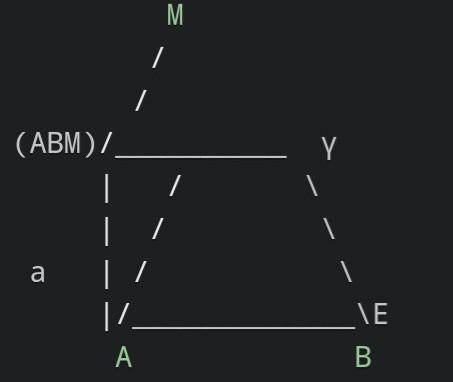
Даны две плоскости а и В и три точки А, В, М, причём точка М принадлежит обеим плоскостям, точки А и В принадлежат соответственно плоскостям а и В. Выясните, имеют ли общие точки плоскость (АВМ) и плоскость ү(гамма), проходящая через линию пересечения плоскостей а и В и точку Е - середину отрезка АВ. Если имеют, то покажите их на чертеже. Объясните свой ответ. (Рисунок обязательно)
Ответы
Так как точка М принадлежит обеим плоскостям, то она принадлежит и плоскости (АВМ). Также, так как точки А и В принадлежат плоскостям а и В соответственно, линия пересечения плоскостей а и В проходит через эти две точки.
Точка Е — середина отрезка АВ, следовательно, она тоже лежит на линии пересечения плоскостей а и В. Из этих фактов можно сделать вывод, что плоскость (АВМ) и плоскость ү проходят через одну и ту же линию (линию пересечения плоскостей а и В) и одну точку — точку М.
Чтобы показать это на чертеже, необходимо нарисовать плоскость (АВМ) и плоскость ү, указав точку М, линию пересечения плоскостей а и В, а также точку Е, как середину отрезка АВ. Ниже приведен чертеж, демонстрирующий общие точки плоскости (АВМ) и плоскости ү:
На чертеже точка М является общей точкой обеих плоскостей, (АВМ) и ү.