Question

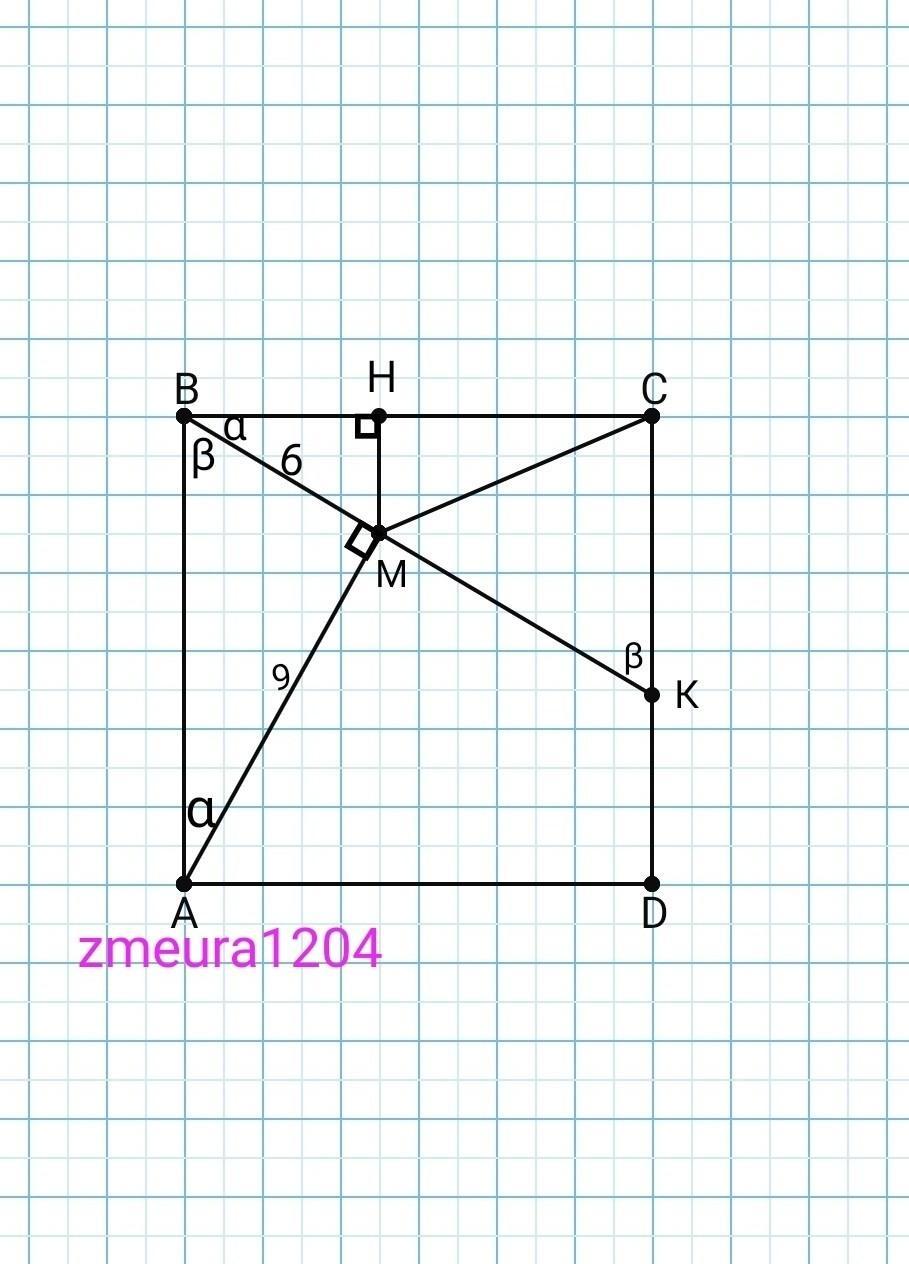
В середині квадрата ABCD проведено ВМ перпендикулярно АМ, так що ВМ-6см і АМ-9см. Знайдіть довжину МС.

Answer 1

Ответ:

МС=√45см

Объяснение:

Розв'язання 1)

∆АВМ- прямокутний трикутник

Теорема Піфагора:

АВ=√(ВМ²+АМ²)=√(6²+9²)=

=√(36+81)=√117см

ВС=√117см

∆АВМ~∆ВКС, за кутами.

МК=х. ВК=(6+х)

АВ/ВК=АМ/ВС

√117/(6+х)=9/√117

9(6+х)=√117*√117

6+х=117/9

х=13-6

х=7 см. МК.

ВК=13см.

∆СКВ- прямокутний трикутник.

Теорема Піфагора:

СК=√(ВК²-ВС²)=√(13²-(√117)²)=

=√(169-117)=√52см.

∆ВНМ~∆ВСК, за кутами.

ВМ/ВК=ВН/ВС

6/13=ВН/√117

ВН=6√117/13.

НС=ВС-ВН=√117-6√117/13=

=13√117/13-6√117/13=7√117/13см.

НМ/СК=ВМ/ВК

НМ/√52=6/13

НМ=6√52/13см.

∆НМС- прямокутний трикутник.

Теорема Піфагора:

МС=√(НМ²+НС²)=

=√((6√52/13)²+(7√117/13)²)=

=√((36*52+49*117)/169)=

=√(1872+5733)/169)=

=√(7605/169)=√45 см

______________

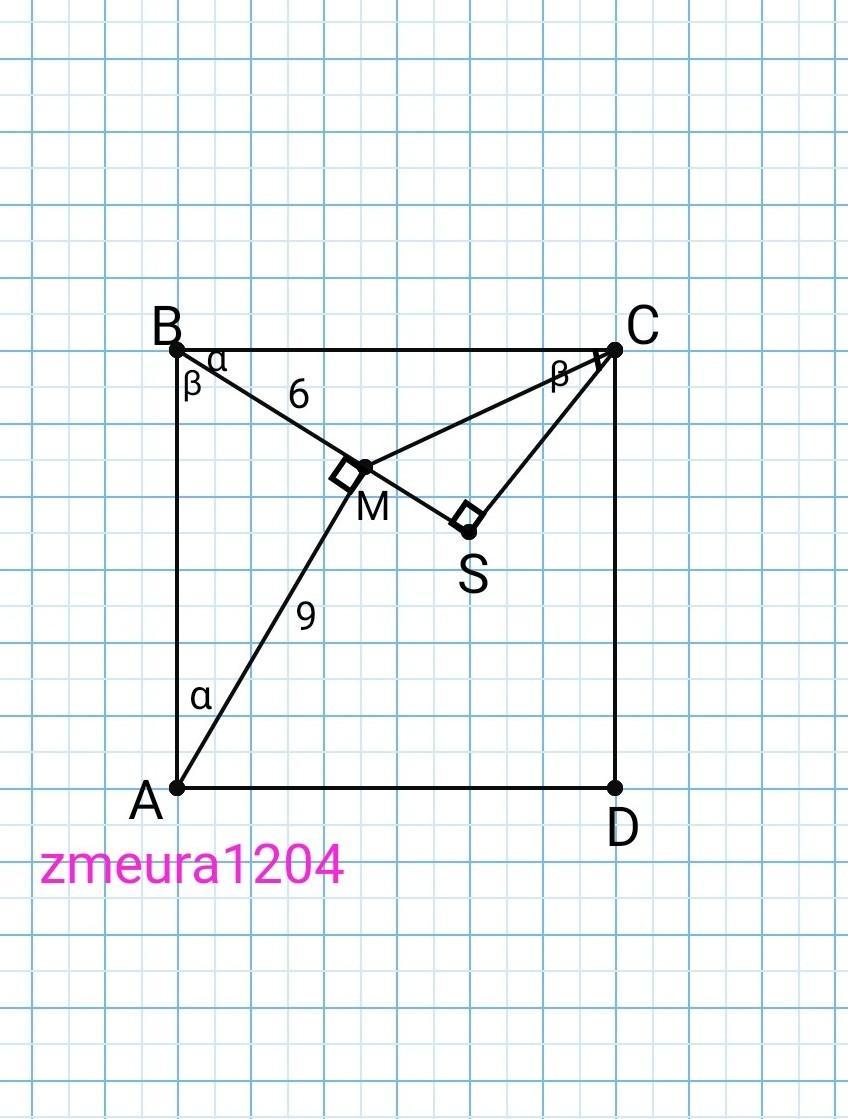
Розв'язання 2)

АВ=ВС=√117см.

∠ВАМ=α; ∠ABM=β.

Побудуємо прямокутний трикутник ∆ВSC.

ВС=АВ гіпотенузи рівні, гострі кути рівні.

∠SBC=∠ABC-∠ABM=90°-β=α.

∠BCS=β.

∆BSC=∆AMB.

BS=AM=9см.

МS=BS-BM=9-6=3см.

SC=BM=6см

∆МСS - прямокутний трикутник.

Теорема Піфагора:

МС=√(MS²+SC²)=√(3²+6²)=

=√(9+36)=√45см