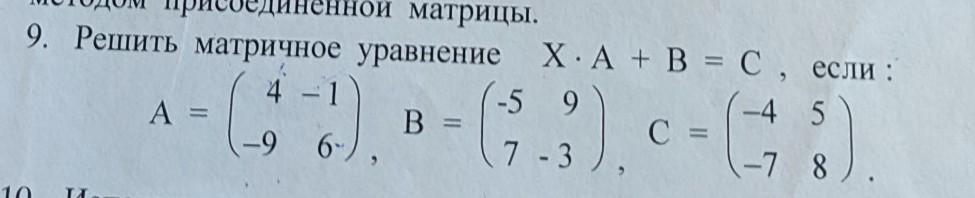Ответы
Ответ дал:
0
Ответ:
Решить матричное уравнение .
Найдём матрицу, обратную матрице А .
Теперь перемножим матрицы и
, получим искомую
матрицу Х .
Приложения:


Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад