Вычисли радиус окружности, описанной _около треугольника, если один из его углов равен 45° а противолежащая ему сторона равна 54 см.
Ответы
Ответ дал:
3
Ответ: 27√2 см .
По теореме синусов имеем :
Приложения:
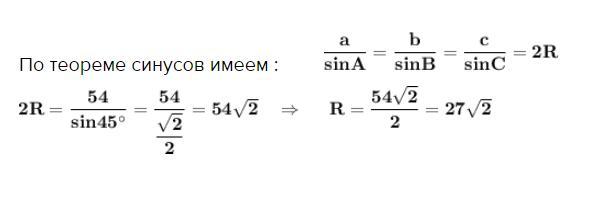
fctdgsygfdhngfxzgsac:
NNNLLL54, здравствуйте! у меня в профиле есть несколько заданий, можете помочь пожалуйста?
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад