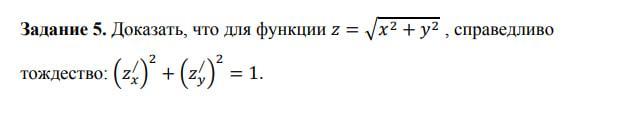Question

Срочно!!!!
Высшая математика. . Доказать, что для функции справедливо
тождество

Answer 1

Ответ:

Для доказательства тождества (z/x)² + (x/y)² = 1, мы можем воспользоваться теоремой Пифагора для прямоугольного треугольника.

Пусть у нас есть прямоугольный треугольник с катетами x и y, и гипотенузой z. Тогда по теореме Пифагора мы имеем:

z² = x² + y²

Теперь мы можем разделить обе стороны этого уравнения на x²y²:

(z/x)² + (y/x)² = (x/y)² + 1

Теперь мы видим, что (z/x)² + (y/x)² это то же самое, что и (x/y)² + 1, что доказывает тождество (z/x)² + (x/y)² = 1.

Пошаговое объяснение:

вот такие пироги