Question

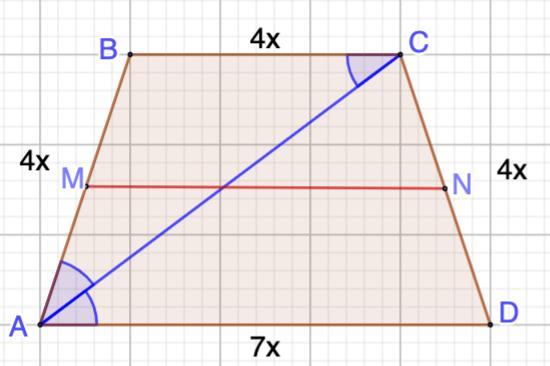
В равнобокой трапеции диагональ АС является биссектрисой, а BCAD=4:7. Найдите среднюю линию MN, если периметр трапеции равен 76 см (рисунок 3).​

Answer 1

Ответ:

Средняя линия MN равна 22 см.

Объяснение:

В равнобокой трапеции диагональ АС является биссектрисой, а BC:AD=4:7. Найдите среднюю линию MN, если периметр трапеции равен 76 см.

Дано: ABCD - равнобедренная трапеция;

АС - диагональ, биссектриса;

ВС : AD = 4 : 7;

Р(ABCD) = 76 см.

MN - средняя линия.

Найти: MN

Решение:

ВС : AD = 4 : 7

Пусть ВС = 4х см, тогда AD = 7x см.

Рассмотрим ΔАВС.

∠ВАС = ∠СAD (условие)

∠ВСА = ∠CAD (накрест лежащие при BC || AD и секущей АС)

⇒ ∠ВАС = ∠ВСА

• Если в треугольнике два угла равны, то он равнобедренный.

⇒  АВ = ВС = 4х см

• Периметр - сумма длин всех сторон трапеции.

Трапеция равнобедренная   ⇒   АВ = CD = 4x см.

P(ABCD) = AB + BC + CD + AD

76 = 4x + 4x + 4x + 7x

19x = 76   |:19

x = 4

⇒   BC = 16 см;   AD = 28 см

• Средняя линия трапеции равна полусумме оснований.

MN = (BC + AD) : 2 = (16 + 28) : 2 = 22 (см)

#SPJ1