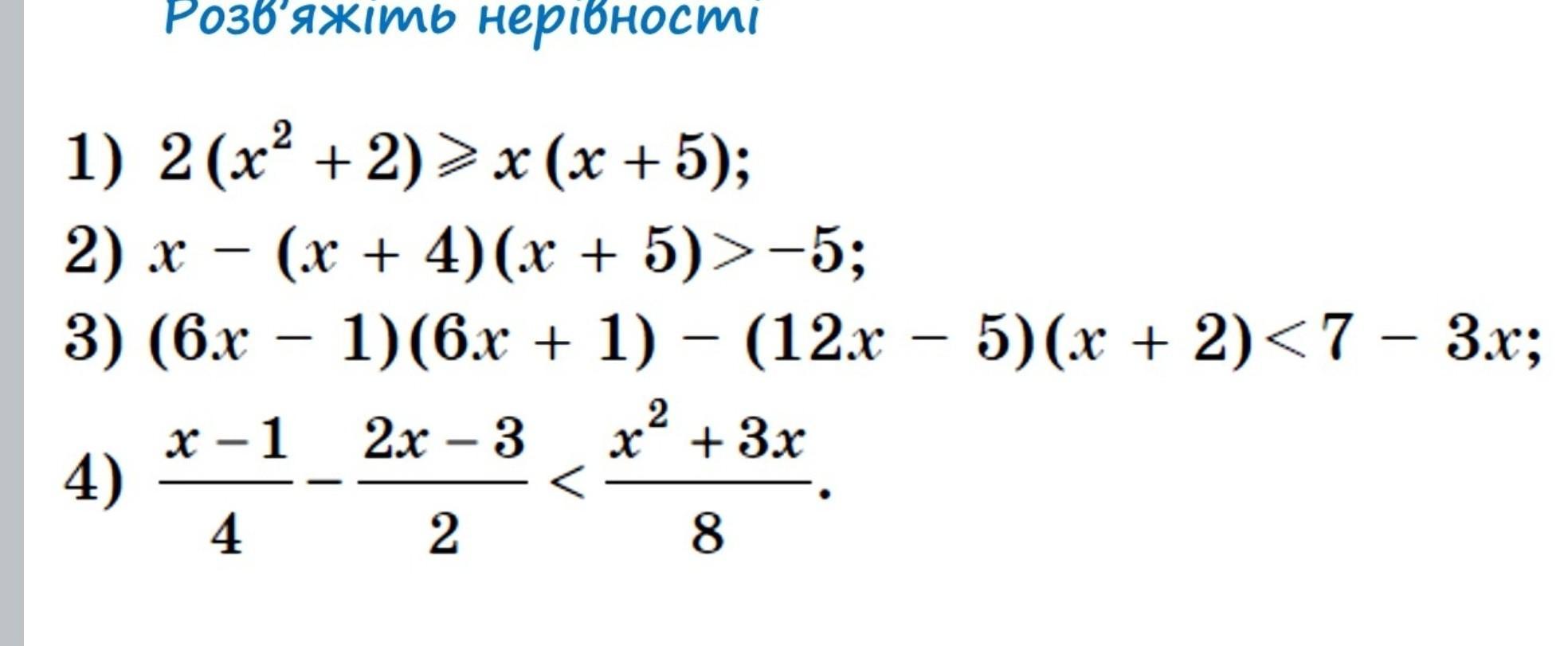Question

математики,допоможіть з алгеброю будь ласка(​

Answer 1

1) 2(x^2 + 2) >= x(x + 5)
2x^2 + 4 >= x^2 + 5x
x^2 - 5x + 4 >= 0

Треба розв'язати квадратну рівняння x^2 - 5x + 4 = 0:

(x - 1)(x - 4) >= 0

Розв'язок: x <= 1 або x >= 4.

2) x - (x + 4)(x + 5) > -5
x - (x^2 + 9x + 20) > -5
x - x^2 - 9x - 20 + 5 > 0
-x^2 - 8x - 15 > 0

Треба розв'язати квадратну рівняння -x^2 - 8x - 15 = 0:

(x + 3)(x + 5) < 0

Розв'язок: -5 < x < -3.

3) (6x - 1)(6x + 1) - (12x - 5)(x + 2) < 7 - 3x
36x^2 - 1 - (12x^2 - 14x + 5x + 10) < 7 - 3x
36x^2 - 1 - 12x^2 + 19x - 10 < 7 - 3x
24x^2 + 22x - 1 < 7 - 3x
24x^2 + 25x - 8 < 0

Треба розв'язати квадратну рівняння 24x^2 + 25x - 8 = 0:

(x + 8)(24x - 1) < 0

Розв'язок: -8 < x < 1/24.

4) (x - 1)/4 - (2x - 3)/2 < (x^2 + 3x)/8
2(x - 1) - 4(2x - 3) < (x^2 + 3x)/2
2x - 2 - 8x + 12 < (x^2 + 3x)/2
-6x + 10 < (x^2 + 3x)/2
4(-3x + 5) < (x^2 + 3x)/2

Треба розв'язати рівняння 4(-3x + 5) = (x^2 + 3x)/2:

-12x + 20 = (x^2 + 3x)/2
-24x + 40 = x^2 + 3x
x^2 + 27x - 40 = 0

Розв'язок: використовуємо квадратне рівняння:

x = (-27 ± sqrt(27^2 - 4(-40)))/(2)
x = (-27 ± sqrt(729 + 160))/(2)
x = (-27 ± sqrt(889))/(2)

Отримали два значення для x: x ≈ -28.95 і x ≈ 1.949.

Таким чином, розв'язок нерівності -28.95 < x < 1.949.