Если можно,с рисунком :]
1) Основанием пирамиды является квадрат,одно из боковых ребер перепендикулярно плоскости основания.Плоскость боковой грани,не проходящей через высоту пирамиды,наклонена к плоскости основания под углом 45 градусов.
Найдите: а) высоту пирамиды; б) площадь боковой поверхности пирамиды.
2) Выcота правильной треугольной пирамиды равна h,а двугранный угол при стороне основания равен 45 градусам.Найдите площадь поверхности пирамиды.
Ответы
а)
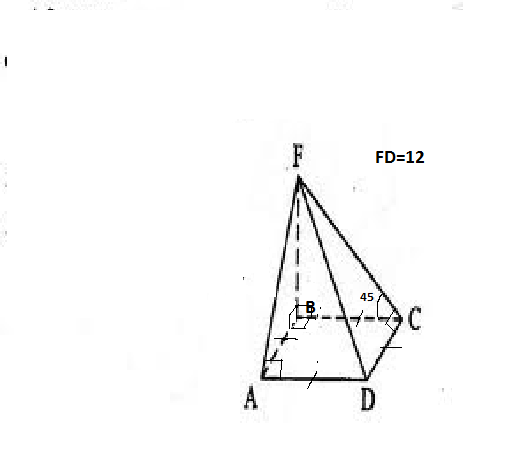
1) Работаем по рис.
Выясним,как расположена высота пирамиды. По определению: высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания.Таким образом, согласно условия задачи, высотой является боковое ребро, перпендикулярное плоскости основания, т.е. FB :
т.к. FB ⊥ (ABC), то FB - высота пирамиды.(1-я цель!!!)
2) Из ΔBCF- прям.: ∠BCF=∠BFC = 45⁰ , значит Δ BCF -равнобедр. и ВС = FB
(!!! Из условия двугранный угол ВСDF (угол между гранями ) равен 45⁰, а его линейным углом является ∠BCF , т.к. ВС ⊥ CD (квадрат)
FC ⊥ CD ( теорема о 3-х перпенд.)).
Тогда FC= FB·√2 (!!! в равноб. прям. тр-ке гипотенуза в √2 раз больше катета)
3)!!!Из четырёх боковых рёбер наибольшим является FD, т.к. является по "совместительству" гипотенузой ΔAFD.Боковая поверхность пирамиды составлена из 4-х прямоугольных тр-ка , причём ΔBCF= ΔBАF ( по двум катетам),
ΔDCF= ΔADF ( по катету и гипотенузе) .
Значит, FD= 12.
4) Из Δ FDC- прям.: FC² +CD²=FD²
Пусть СD=BC=FB= x, тогда ( x√2)²+x²=12²
2x²+x²=144
3x²=144
x²=48
x=√48=4√3(cм)
FC= 4√3 cм = высота.
б) Площадь боковой поверхности пирамиды равна сумме площадей боковых граней, а о том , что представляют собой грани сказано выше. Стоит отметить , что равные фигуры имеют равные площади, тогда
S =2·S abf + 2·S cdf = 2·( ½·AB·BF+½·CD·CF)= 4√3·4√3 +4√3·4√6= 48 +16√18=
= 48 +48√2 =48·(1+√2) cм².