допоможіть! будь ласка, з повним рішенням!
-6х⁷y⁵×(-1 1/6x-²y-²)
(-2/5a⁵b)× 15/16 a-⁷ b-⁴
Приложения:
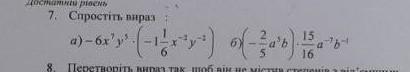
Ответы
Ответ дал:
3
Ответ:
Объяснение:
Свойство степеней: .
Решение. Раскроем скобки и применим свойство степеней.
#SPJ1
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
https://znanija.com/task/54583924