Question

Периметр паралелограма дорівнює 54см. Знайдіть сторони паралелограма, якщо дві з них відносяться як 4:5.

Answer 1

Ответ:

Сторони паралелограма дорівнюють 12см, 15см, 12 см, 15 см.

Объяснение:

УМОВА:

Периметр паралелограма дорівнює 54см. Знайдіть сторони паралелограма, якщо дві з них відносяться як 4:5.

РОЗВ'ЯЗАННЯ:

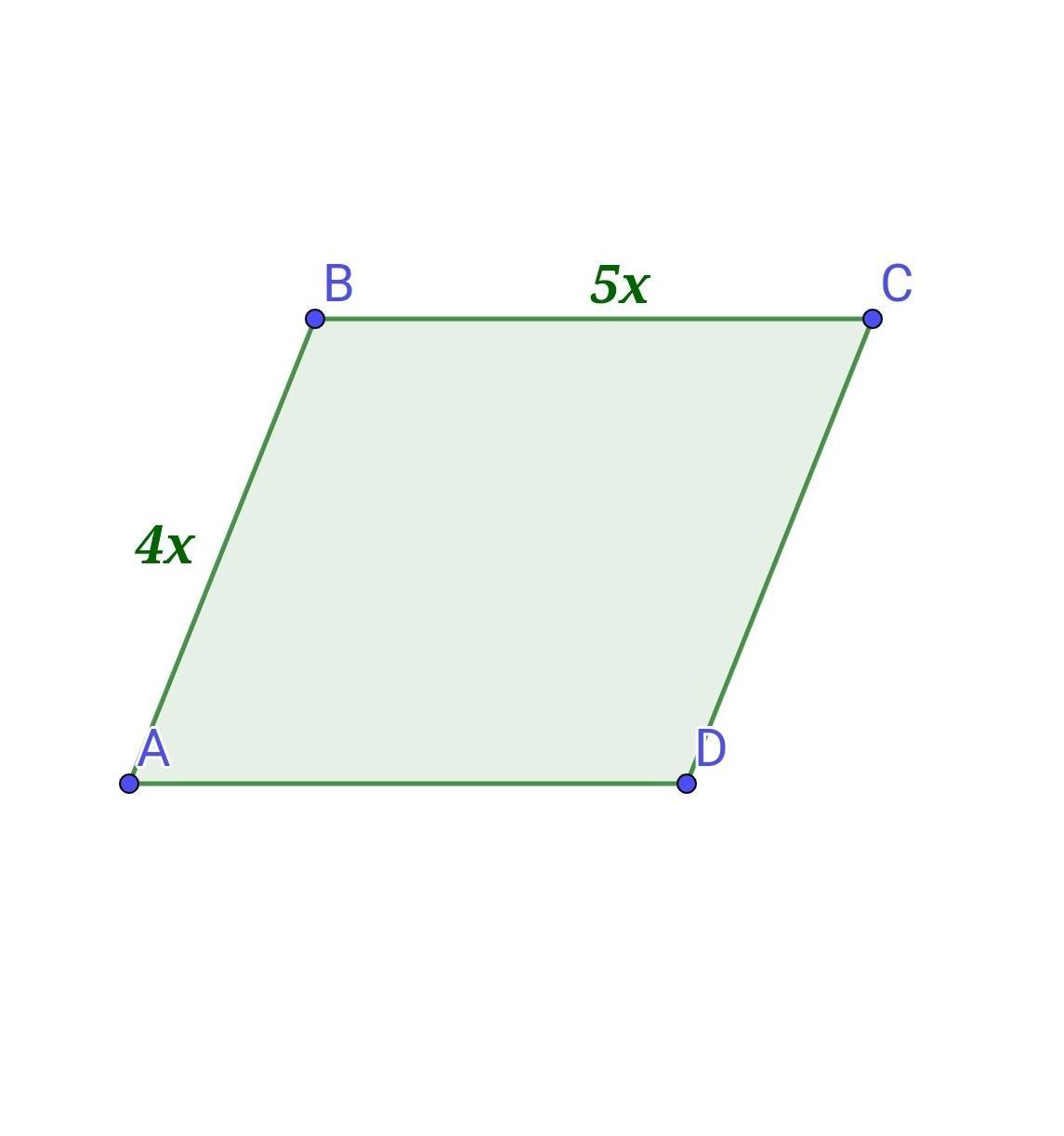
Нехай ABCD - даний паралелограм, Р(ABCD)=54 см.

Так як протилежні сторони паралелограма рівні, то в умові задачі маємо сусідні сторони.

Нехай AB=4х, ВС=5х, де х - коефіцієнт пропорційності.

Тоді периметр паралелограма:

Р(ABCD) = 2 • (AB + BC)

2•(4х+5х)=54

9х=54:2

9х=27

х=3

Отже, АВ=4•3=12(см); ВС=5•3=15(см).

CD=AB=12(см) - як протилежні сторони паралелограма.

AD=BC=15(см) - як протилежні сторони паралелограма.

ВІДПОВІДЬ: АВ=СD=12 см, BC=AD=15 см

#SPJ1