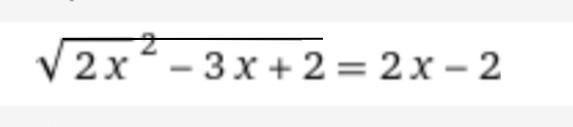Question

Решите уравнение пожалуйста

Answer 1

Ответ:

x = 2

Объяснение:

$\sqrt{2x^2-3x+2} =2x-2$

При решении подобных иррациональных уравнений важно знать следующий равносильный переход:

$\sqrt{f(x)} =g(x)$ ⇔ $\left \{ {{f(x)=g(x)^2} \atop {g(x)\geq 0}} \right.$

Почему в системе мы помимо того, что g(x) должно быть больше или равно 0, не указываем также, что f(x) должно быть больше или равно 0? Потому что это условие автоматически выполняется, когда мы g(x) возводим в квадрат, так как тогда f(x) мы приравниваем к квадрату какого-то числа, то есть заведомо положительному числу (или нулю).

Воспользуемся переходом выше и решим наше уравнение:

$\left \{ {{2x^2-3x+2=(2x-2)^2} \atop {2x-2\geq 0}} \right. \\\left \{ {{2x^2-3x+2=4x^2-8x+4} \atop {x\geq 1}} \right.\\4x^2-8x+4-2x^2+3x-2=0\\2x^2-5x+2=0\\x_{1,2}=\frac{5+-\sqrt{(-5)^2-4*2*2} }{2*2} =\frac{5+-3}{4} =(2;0.5)$

Проверим наши корни:

x₁ = 2 нам подходит, поскольку удовлетворяет условию 2x - 2 >= 0.

x₂ = 0.5 нам не подходит, поскольку не удовлетворяет условию 2x - 2 >= 0.