Ответы
Ответ:
Объяснение:
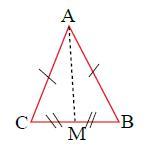
Дано:
Р(Δавс) = 72см
АВ = АС
АМ - медиана,
АМ = 12см
___________
Р(Δавм)- ?см
Р(Δавм) = АВ+АМ+MB = АВ + 12 + СВ/2 (т.к. АМ - медиана, то
СМ = МВ = СВ/2)
2Р(Δавм) = 2АВ +2*12 +СВ, но
2АВ + СВ = АВ +АС + СВ = Р(Δавс) = 72
2Р(Δавм) = 72 +2*12
Р(Δавм) = 72*2+12= 36 +12 = 48(см)
Р(Δавм) = 48см
1б.
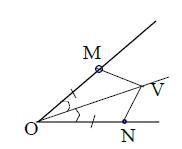
Дано:
ОМ = ON
OV - биссектриса ∠MON
Док., ΔOMV = ΔONV
----------------
Рассм., ΔOMV и ΔONV
ОМ = ON по условию,
∠MOV = ∠NOV, т.к. OV - биссектриса
OV - общая сторона
ΔOMV = ΔONV по 2-м сторонам и углу между ними (1-ый признак равенства Δ-ков)
2б-1
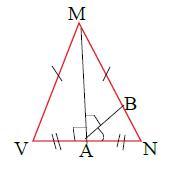
Дано:
ΔMNV
MV = MN
MA - медиана ΔMNV
АВ - биссектриса ∠MAN
∠VAB - ?
В равнобедренном Δ-ке медиана является одновременно высотой и биссектрисой, поэтому
∠MAV =90°
∠МАВ = 45°, т.к. АВ - биссектриса ∠MAN=90°
∠VAB = ∠MAV + ∠МАВ= 90° + 45° = 135°
∠VAB = 135°
3б
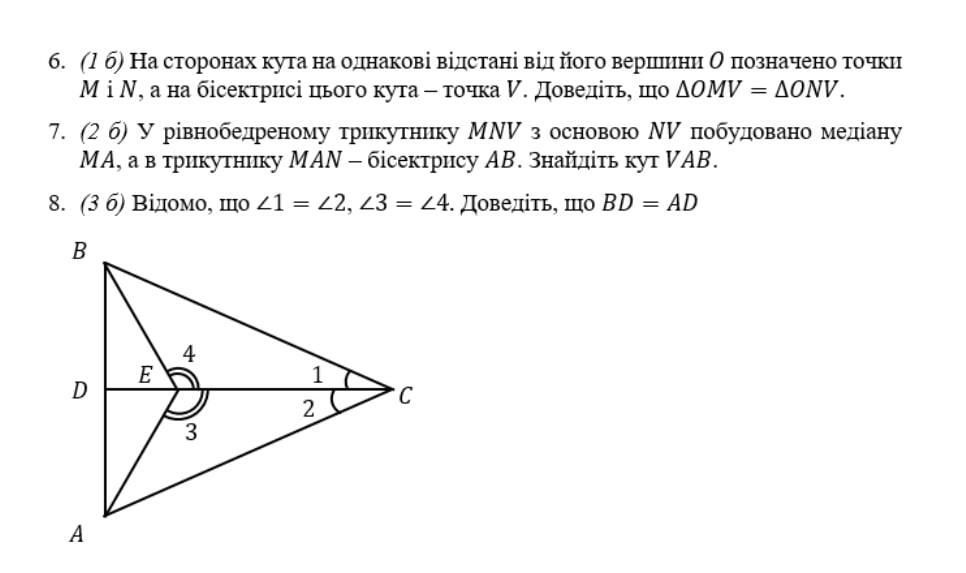
1) Рассмотрим ΔВЕС и ΔАЕС
∠1 = ∠2 и ∠4 = ∠3 по условию
ЕС - общая сторона
ΔВЕС = ΔАЕС по стороне и двум прилежащим к ней углам (2-ой признак равенства Δ-ков). Следовательно,
ВЕ = АЕ
2) ∠BED - смежный с ∠ВЕС, ∠BED = 180° - ∠ВЕС
∠AED - смежный с ∠АЕС, ∠AED = 180° - ∠АЕС
Т.к. ∠ВЕС = ∠АЕС (по условию), то и
∠BED = ∠AED
3) Рассм. ΔBED и ΔAED
∠BED = ∠AED, ВЕ = АЕ, DE - общая сторона.
ΔBED = ΔAED по двум сторонам и углу между ними (1-ый признак равенства Δ-ков). Следовательно, и
BD = AD, ч.т.д.