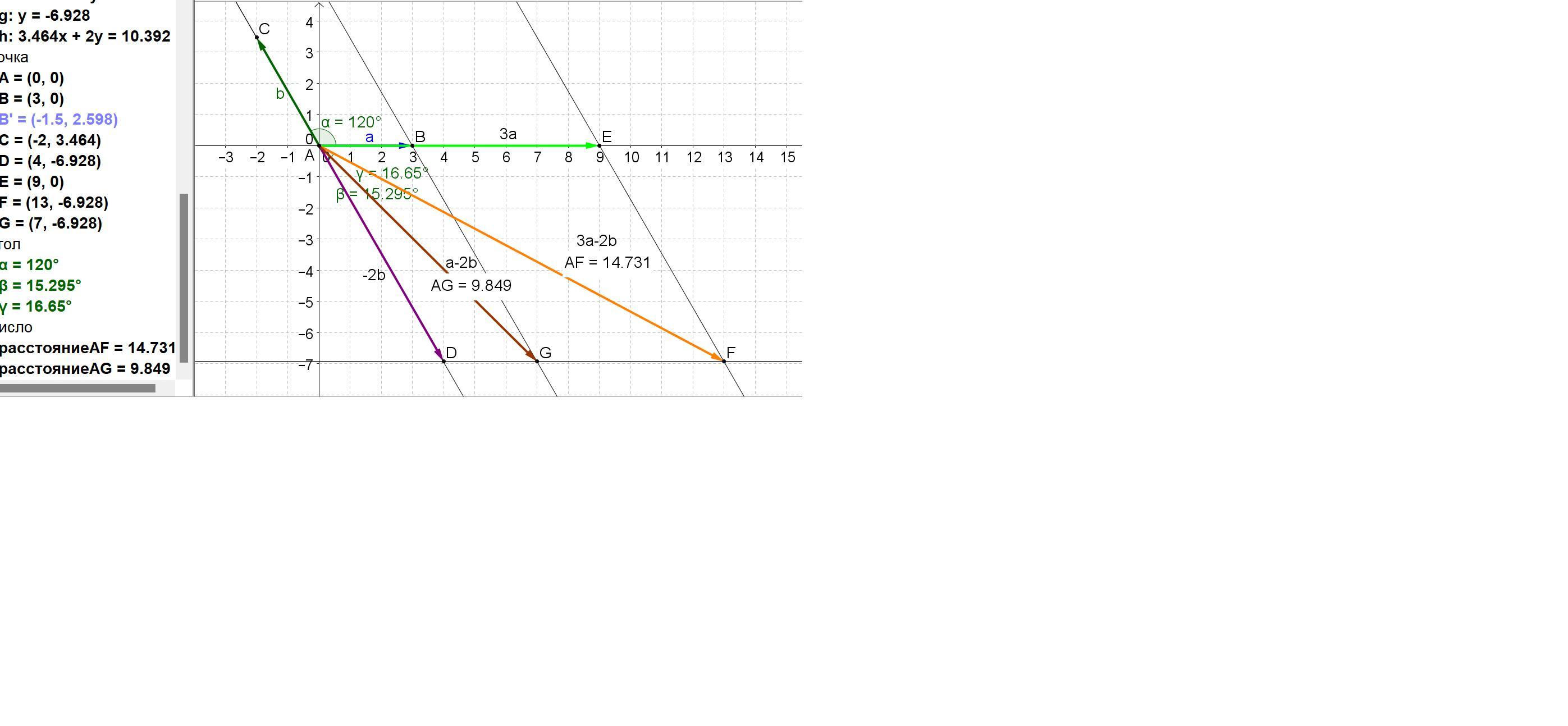
Ответы
Модуль (3a – 2b) = √((3*3)² + (4*2)² - 2*9*8*cos(2π/3)) =
= √(81 + 64 – 144*(-1/2)) = √217.
Модуль (a – 2b) = √(3² + (4*2)² - 2*3*8*cos(2π/3)) =
= √(9 + 64 – 48*(-1/2)) = √97.
Находим углы между векторами и общим вектором (–2b).
cos(α1) = ((4*2)² + (√217)² - (3*3)²)/(2*8*√217) = 0,8486.
α1 = arccos(0,8486) = 31,945 градуса.
cos(α2) = ((4*2)² + (√97)² - 3²)/(2*8*√97) = 0,9646.
α2 = arccos(0,9646) = 15,295 градуса.
Отсюда находим угол между векторами.
α = α1 – α2 = 31,945 - 15,295 = 16,65 градуса.
Так как в задании не оговорено, какое произведение векторов:1) скалярное или 2) векторное, то рассмотрим оба варианта.
1) Скалярным произведением двух векторов называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними. Длина вектора является его модулем.
(3a – 2b)(a – 2b) = √217*√97*cos(15,295°) = 139.
2) Векторным произведением векторов a и b называют перпендикулярный им вектор c из правой тройки, модуль которого равняется произведению модулей векторов a и b на синус угла между ними.
(3a – 2b)x(a – 2b) = √217*√97*sin(15,295°) = 41,569.