Ответы
Ответ дал:
1
Ответ:
Найти производные функций . Применяем правила дифференцирования и таблицу производных .
Приложения:

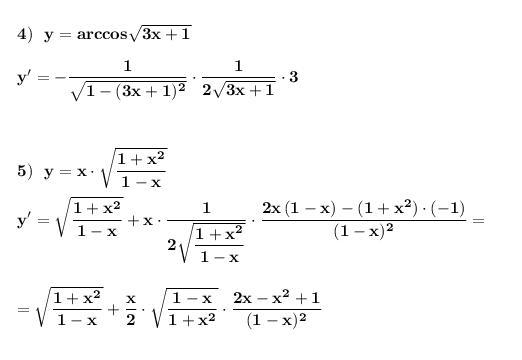


Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
8 лет назад
