Двоє робітників, працюючи разом, виконали виробниче завдання за 12 год. За скільки годин може виконати це завдання кожен робіт ник, працюючи самостійно, якщо перший із них може це зробити на 10 год швидше, ніж другий?
Ответы
Ответ дал:
0
Ответ: 20 ч , 30 ч .
Пусть 1 работник выполнит задание за х часов .
Тогда 2 работник выполнит это задание за (х+10) часов .
Производительность 1 работника равна 1/х части задания за 1 час .
Производительность 2 работника равна 1/(х+10) части задания за 1 час .
Совместная производительность равна
Отрицательное значение х = -6 по смыслу задачи не подходит .
Первый работник может выполнить задание за 20 часов , а второй -
за х+10= 30 часов .
Приложения:
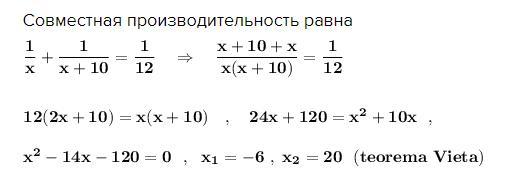
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад