Ответы
Ответ дал:
0
Ответ:
Найти предел функции . Неопределённость вида 0/0 . Раскладываем числитель на множители .
Приложения:
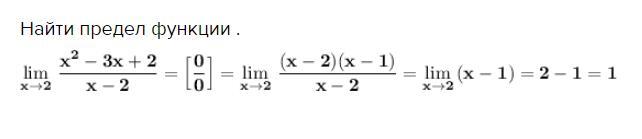
HumanbyBrain:
неправильно ответа нет типо Ответ: 9 или другое
всё правильно
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад