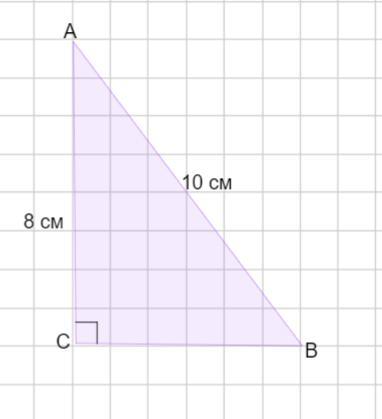
В треугольнике АВС угол С прямой. Гипотенуза АВ равна 10 см, сторона АС равна 8 см. Найдите площадь треугольника АВС.
Ответы
Ответ дал:
2
Ответ:
24 см².
Объяснение:
В треугольнике АВС угол С прямой. Гипотенуза АВ равна 10 см, сторона АС равна 8 см . Найти площадь теугольника АВС
По условию задан ΔАВС - пряямоугольный ( ∠С =90°) .
Катет АС = 8 см, гипотенуза АВ =10 см.
Найдем второй катет ВС . Для этого воспользуемся теоремой Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
АВ ² = АС² +ВС²;
ВС² = АВ² - АС²;
ВС² = 10² - 8² = 100- 64 = 36;
ВС =√36 = 6 см.
Найдем площадь прямоугольного треугольника как полупроизведение катетов.
Площадь данного треугольника равна 24 см².
#SPJ1
Приложения:
Аноним:
ты конечно молодец. Но блят мне уже это не надо
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад