10 номер
изменить порядок интегрирования в повторном интеграле,вычислить его рациональным способом
Приложения:
Ответы
Ответ дал:
0
Ответ:
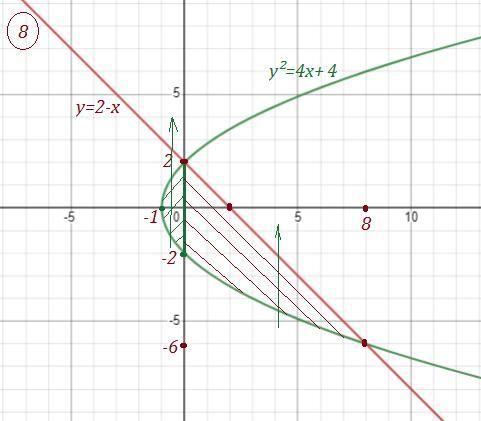
Изменить порядок интегрирования .
Область интегрирования : .
Найдём точки пересечения прямой и параболы
Заданная область проектируется на ось ОУ в отрезок [-6 ; 2 ] . Если меняем порядок интегрирования , то получим две области, которые проектируем на ось ОХ .
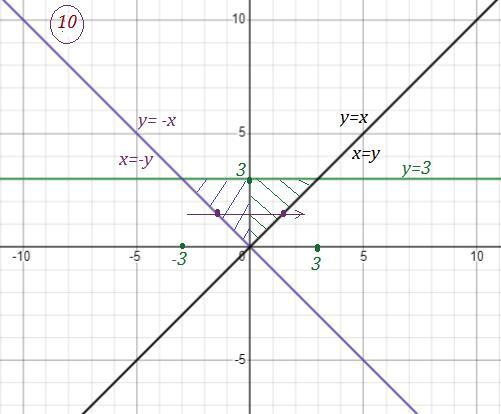
Вычислим повторный интеграл наиболее удобным способом .
Две области интегрирования :
Если спроектировать эти две области на ось ОУ , то получим один отрезок [ 0 ; 3 ] .
Приложения:


Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад