Один из корней уравнения равен 5. Найдите параметр а и второй корень уравнения (используя т. Виета):
x^2 + x - a=0
Помогите дам 50б
Приложения:
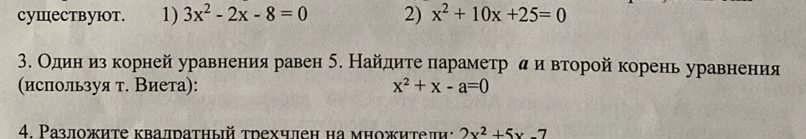
Ответы
Ответ дал:
1
Ответ:
, второй корень равен
Объяснение:
По теореме Виета , где
- корни уравнения
Имеем , следовательно получаем
. А подставив это во второе уравнение, получим, что значение параметра
равно
.
Окончательный ответ: .
P. S. Ну а само уравнение имеет вид , корнями которого, действительно, являются числа
и
.
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад